 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теоретический материал |  |
Reading materials | ||||||||||||||||||||||||||||||||||||||||||||||||||
Web-версия учебного курса "Основы математической статистики"
 Раздел 3.7. Дисперсионный анализ. Проверка гипотезы об отсутствии влияния факторов на параметрВ практике экспериментальной работы мы часто сталкиваемся с необходимостью установить, влияют ли какие-либо условия проведения эксперимента или технологического процесса (факторы) на величину, характеризующую результат эксперимента или процесса (параметр). Мощным средством решения этого вопроса служит дисперсионный анализ. Эксперимент для проведения дисперсионного анализа может быть специально спланирован, но метод применим и для обработки "пассивного" эксперимента, в котором накоплено достаточное количество данных. Для начала рассмотрим пример. Предположим, в нашем распоряжении имеются данные о светоотдаче шестнадцати металлогалоидных ламп, причем лампы группируются в четыре серии, и различие между сериями состоит в том, что при изготовлении в горелки введены различные количества металлического индия. Проиллюстрируем на этом примере, как с помощью однофакторного анализа можно выяснить, влияет ли концентрация индия - это в нашем случае фактор - на светоотдачу горелок (параметр). В таблице 3.5 представлены результаты измерения светоотдачи (в лм/Вт). Уровни фактора: 1, 2, 3, 4 - в данном случае это дозировки индия 0.24; 0.43; 0.75; 1 мг. Таблица 3.5. Значения светоотдачи для образцов ламп (лм/Вт)
Введем обозначения: х ji - значение параметра, стоящее в таблице в j-той строке и в i-том столбце (у нас светоотдача лампы номера j из серии номера i);
- среднее значение всех чисел в столбце i (у нас средняя светоотдача
при определенной дозировке индия),
для удобства дальнейших расчетов вычислим эти величины и занесем
в таблицу; 
- среднее для всех чисел в таблице
(генеральное среднее); ri - число опытов , при каждом уровне фактора.
0 состоит в том, что фактор - дозировка индия - не влияет на светоотдачу. Тогда все хji - в таблице - выборка значений одной и той же случайной величины х.
Суть дисперсионного анализа (как однофакторного, так и многофакторного) состоит в том, что строятся различные оценки дисперсии х, и по критерию Фишера проверяется, справедливость гипотезы о том, что это оценки одной и той же дисперсии, т.е. фактор не влияет на параметр. Разумеется, как мы увидим ниже, эти оценки строятся так, чтобы, если влияние фактора есть, то оно бы себя проявило. Если гипотеза Н 0 отвергается, то мы признаем, что фактор влияет на параметр.По данным таблицы 3.5 вычисляем величины Q, Q 1, Q2 по формулам:
Можно показать аналитически и непосредственным вычислением на конкретном примере, что
Q - это сумма квадратов отклонений всех чисел в таблице от генерального среднего. Если все они принадлежат выборке значений одной нормально распределенной величины с дисперсией σ 2 (иногда говорят: "одной генеральной совокупности"), т.е. фактор не влияет на результат, то, согласно (2.1)Q / σ2 ~ Χ2n-1, где n - полное число данных в таблице.  
Q2 - характеризует случайный разброс результатов внутри одного уровня фактора. Каждое слагаемое в Q2 / σ2 распределено по закону ~ Χ2 с числом степеней свободы ri - 1, следовательно, Q2 / σ2 ~ Χ2n-v. Q1-
характеризует, как видно из определения, именно влияние фактора.
Но если этого влияния нет, то каждое (Легко видеть, что, как и следует из (3.15), сумма числа степеней свободы для Q2 / σ2 и Q1 / σ2 равна числу степеней свободы для Q / σ2). Таким образом, проверка гипотезы об отсутствии влияния фактора сводится к проверке гипотезы о равенстве дисперсий, оцененных сначала как
затем как
Гипотеза проверяется по критерию Фишера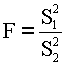 
Выбрав уровень значимости α, находим по таблице F-распределения границу критической области Fq, такую что при числе степеней свободы к1 = ν - 1, к2 = n - ν P{1 / Fq > F или F > Fq} = α. Если экспериментальное значение F < Fq, то гипотеза принимается, т.е. фактор не влияет на результат. (Если в данном случае окажется, что S12 < S22, то, учитывая смысл этих величин, следует сделать вывод, что фактор не влияет, даже, если критерий попадет в критическую область. Ведь это возможно и при справедливости гипотезы с вероятностью α). Выполним расчеты для приведенного примера. Q = (100 - 92.125)2 + (97 - 92.125)2 + ... + (85 - 92.125)2 = 439.75 (всего 16 слагаемых) Q1= 5(96.2 - 92.125)2 + 4(93.5 - 92.125)2 + 4(87.25 - 92.125)2 + 3(90 - 92.125)2 = 199.2 Q2 = Q - Q1 = 240.55 n = 16, v = 4, соответственно, число степеней свободы для Q1 равно 3, для Q2 равно 12, отсюда S 12 = Q1 / 3 = 66.4, S22 = Q2 / 12 = 20.05.Fэ = S12 / S22 = 3.312, Fq(k1 = 3, k2 = 12, α = 0.05) = 3.49. Fэ < Fq. Гипотеза Н0 принимается, дозировка индия в указанных пределах не влияет на светоотдачу. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
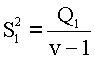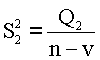(3.12)
(3.13)
(3.14)
,
.