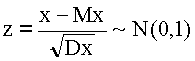| Теоретический материал | Reading materials | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Web-версия учебного курса "Основы математической статистики"
Раздел 3.5. Проверка гипотезы о законе распределения случайной величины3.5. Проверка гипотезы о законе распределения случайной величины
Существует несколько способов проверки справедливости предположений о законе распределения cлучайной величины [5]. Рассмотрим наиболее распространенный и наглядный способ, в котором в качестве критерия используется уже известное распределение Χ2. Предположим, имеется выборка n значений случайной величины x. Объем выборки (n) должен быть велик - не менее нескольких десятков значений. Гипотеза Н0 состоит в том, что случайная величина x распределена по некоторому определенному закону с плотностью распределения р(х), например, нормально или равномерно, или как угодно - непрерывно или дискретно, но закон распределения известен.Критерием проверки такой гипотезы может служить случайная величина Χ 2 . Закон распределения величины Χ2 нам известен.Покажем, как строится этот критерий в данном случае. Будем сразу пояснять алгоритм на примере. Предположим, в некоторую систему встроен генератор случайных чисел, который должен генерировать действительные числа, равномерно распределенные в интервале (0, 1). Требуется проверить, отвечает ли генератор этому требованию. Ниже приведена выборка, состоящая из 100 значений, выработанных генератором (табл. 3.2). Таблица 3.2. Значения
случайной величины, выработанные генератором случайных чисел
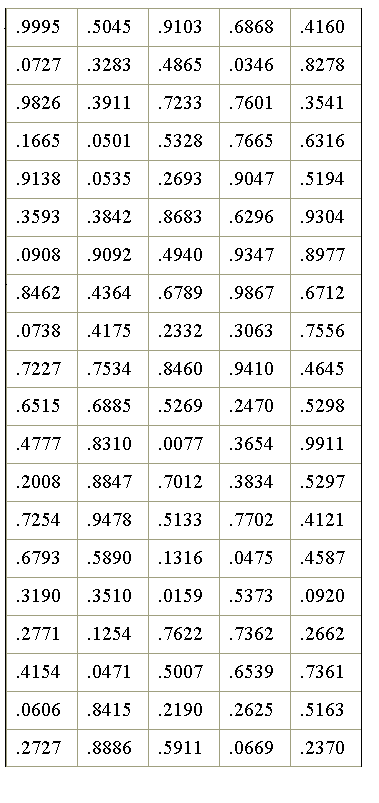 Гипотеза Н 0: распределение равномерно в интервале (0, 1).Мы видим, что, действительно, ни одно число из выборки за пределы этого интервала не выходит, поэтому считаем, что весь диапазон изменения x простирается от 0 до 1. Разобьем этот диапазон на интервалы, количество их выберем так, чтобы в среднем на каждый приходилось около 10 элементов выборки и, соответственно, чтобы теоретическая вероятность попадания в каждый интервал не была мала. (см. табл. 3.3).Таблица 3.3. Анализ функции распределения по выборке, представленной в табл. 3.2
n = 100, число интервалов L в нашем случае равно 10. В третий столбец таблицы введены предсказанные нашей гипотезой вероятности рi попадания в i-тый интервал, а в четвертый столбец - реальное число элементов выборки mi, попавших в этот интервал. Теперь рассмотрим каждую строку
таблицы отдельно. Произведено всего n = 100 независимых испытаний,
вероятность события, например, попадания во второй интервал
(т.е. от 0.1 до 0.2), рi = 0.1.
Число mi попаданий
в этот интервал - случайная величина, распределенная по закону Бернулли
[6]. При большом n величина В табл.3.3 в пятом столбце помещены экспериментальные величины η i.Вычислим 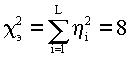 .
Выбрав уровень значимости
α = 0.05,
обратимся к таблицам Χ2-распределения,
чтобы найти критическую область Q.
Она будет односторонней. Действительно, малая сумма Χ2э
означает, что mi
очень близко к nрi,
т.е. реальное число попаданий в интервал близко к математическому
ожиданию числа попаданий. Это означает справедливость наших
предположений о значениях рi,
т.е. гипотеза Н0
подтверждается. .
Выбрав уровень значимости
α = 0.05,
обратимся к таблицам Χ2-распределения,
чтобы найти критическую область Q.
Она будет односторонней. Действительно, малая сумма Χ2э
означает, что mi
очень близко к nрi,
т.е. реальное число попаданий в интервал близко к математическому
ожиданию числа попаданий. Это означает справедливость наших
предположений о значениях рi,
т.е. гипотеза Н0
подтверждается.
Отвергать ее будем лишь при большом по абсолютной величине отличии m i от nрi. В нашем примере ν = 10 - 1 = 9, Χ2q (α = 0.05) = 16.9.Вывод: Χ 2э < Χ2q. Гипотеза о том, что исследуемое распределение равномерно, проверена по критерию Χ2 на уровне значимости 5% и принята.При проверке предположения о нормальном законе распределения могут возникнуть два случая: 1) Параметры этого закона Mx и Dx (математическое ожидание и дисперсия) предполагаются известными, т.е. Н 0: х ~ N(Mx, Dx), в этом случае удобно ввести новую случайную величину
Пользуясь таблицами нормального распределения, легко найти вероятность попадания z в интервалы, которые выбрать заранее. При этом надо следить, чтобы вероятность попадания в каждый интервал не была очень малой, например, в качестве первого взять интервал от -∞ до -2. Вероятность попадания в интервал вычисляется с помощью интеграла вероятностей Ф(z), как разность значений Ф(z) от концов интервала (см. таблицы нормального распределения). Получим, например, следующие вероятности, представленные в табл. 3.4. Таблица 3.4. Интервалы значений случайной величины z ~ N(0, 1) и вероятности pi попадания в эти интервалы
Теперь можно либо пересчитать все величины выборки x в z по формуле (3.7), либо пересчитать концы интервалов и найти, сколько реально значений х попадает в данный интервал. Дальнейшие действия аналогичны описанным в примере с равномерным распределением. Критерий Χ2 имеет L - 1 степеней свободы, где L - число интервалов. 2) Если распределение предполагается нормальным, но параметры его Мх и Dх не известны, то находят их оценки из той же выборки по формулам (1.1, 1.2). Гипотеза Н 0:Дальнейший алгоритм полностью аналогичен предыдущему случаю, только для критерия Χ2 берется ν = L - 3 степени свободы, т.к. наложены уже 3 связи на величины ηi (оценки матожидания и дисперсии вычислены из элементов той же выборки). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
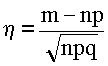 ~ N(0, 1).
Очевидно, что сумма квадратов
таких независимых величин должна иметь распределение Χ2
и поэтому может быть критерием проверки нашей
гипотезы. Число степеней свободы
для критерия берется на 1 меньше, чем число интервалов
(ν = L - 1), т.к. на величины ηi
в данном случае наложена одна связь:
~ N(0, 1).
Очевидно, что сумма квадратов
таких независимых величин должна иметь распределение Χ2
и поэтому может быть критерием проверки нашей
гипотезы. Число степеней свободы
для критерия берется на 1 меньше, чем число интервалов
(ν = L - 1), т.к. на величины ηi
в данном случае наложена одна связь: