Задачи, имеющие принципиальное математическое решение, но неразрешимые вследствие слишком большого влияния случайных погрешностей измерений, получили название "некорректных", точнее "некорректно поставленных" задач.

Для решения такого рода задач, разработаны общие приемы, получившие название "методы статистической регуляризации" [7]. Суть их состоит во внесении в сам процесс решения некоторой априорной (до опыта) информации о виде искомого распределения. Прежде всего, следует отметить, что метод наименьших квадратов по существу также представляет простейший прием статистической регуляризации. Ведь здесь мы предполагаем, что искомая зависимость описывается кривой, определяемой относительно небольшим числом параметров (m) и за счет измерения в большем числе экспериментальных точек (n) можем получить достаточно "устойчивое" решение.

Уменьшение числа искомых коэффициентов b неуклонно ведет к повышению "точности" их определения. Но это совсем не значит, что решение с наименьшим числом параметров и будет наилучшим; оно будет наименее чувствительным к погрешностям эксперимента, но при этом может быть неадекватным, т.е. практически не описывает результат данного эксперимента. Если "устойчивость" решения, т.е величина относительной погрешности коэффициентов модели при минимальном m, при котором решение еще адекватно, нас удовлетворяет, то мы можем ограничиться методом наименьших квадратов, как единственным приемом статистической регуляризации.

Однако, такое положение складывается не всегда. В задачах, связанных с поиском каких-либо распределений, например, зависимости яркости свечения источника от длины волны, если спектр искажен прибором, имеющим конечную разрешающую способность, мы часто заинтересованы в том, чтобы получить информацию о значениях искомой величины в возможно большем числе точек, т.е. стремимся по возможности увеличить число искомых коэффициентов модели, но при этом, естественно, падает их устойчивость по отношению к погрешностям эксперимента.

В этих случаях используется прием регуляризации, основанный на наших вероятностных представлениях о свойствах искомого распределения. Эти представления складываются у нас на основании предыдущего опыта исследования аналогичных объектов или на основании теоретических соображений и потому называются априорными.

Эксперимент вносит уточнения в наши представления об объекте и в результате формируется апостериорное (после опыта) распределение вероятностей для значений коэффициентов модели. Искомое решение получается в результате усреднения всевозможных значений искомых коэффициентов с учетом апостериорного распределения их вероятностей, соответственно погрешность решения -это результат усреднения с тем же распределением вероятности квадрата отклонения всевозможных значений коэффициентов от средних значений.

Математическое оформление изложенного метода решения, разумеется, зависит от характера использованной априорной информации о решении. Для многих задач весьма успешно может быть применен прием, основанный на априорном предположении о принадлежности решения к классу достаточно "гладких" или "ограниченных" функций; в этих случаях искомые коэффициенты модели находятся из системы уравнений:

Здесь матрицы y, А, W, b имеют прежний смысл (см. раздел 4).

Эти выражение отличается от обычного решения по методу наименьших квадратов слагаемым α Q, которое как раз и заключает в себе априорную информацию о решении. Q - это матрица регуляризации. Мы должны сформировать ее, исходя из априорных представлений о свойствах искомого распределения.

Например, если мы предполагаем, что распределение b(х) должно быть "гладким", а "гладкость" мы математически выражаем как ограниченность n-ной производной - обычно второй, то Q находится из условия: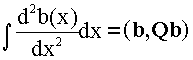

                                         .                                (7.3)

Интеграл берется по всей области определения. Выражение, стоящее справа в (7.3), означает скалярное произведение векторов b и Q b, т.е.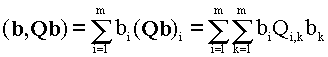

                      .                 (7.4)

Преобразуя левую часть (7.3) так, чтобы входящий туда интеграл заменить конечной суммой, а производную - конечными разностями значений b_i в заданных точках x_i, отнесенными к интервалам x_i+1 - x_i, мы можем левую часть (7.3) представить также, как и в (7.4), в виде суммы слагаемых, содержащих произведения b_i и b_k. Коэффициенты при этих произведениях приравняем к удвоенным элементам матрицы Q (с тем, чтобы Q_ik = Q_ki). В частном случае, когда ограничивается норма второй производной и точки, в которых определяются значения искомой функции, делят весь отрезок задания функции на равные части Δx матрица Q имеет вид:

             .          (7.5)

Размерность ее всегда m * m, где m - число искомых коэффициентов. Параметр регуляризации α - это число, которое показывает, сколь жесткие требования мы накладывает на принадлежность решения к заданному классу функций; чем больше α, тем меньше допустимые значения функционалов, записанных в левой части (7.3). В предельном случае (α = 0) на эти величины не накладывается никаких ограничений, и мы приходим к методу наименьших квадратов. При очень больших α мы приходим к требованию равенства нулю второй производной и решение всегда будет иметь вид линейной зависимости b(х). В то же время устойчивость коэффициентов модели будет неуклонно расти с ростом α, так как погрешность коэффициентов модели, согласно (7.2), будет убывать. Следовательно, решающим становится правильный выбор α: чем больше α, тем больше априорной информации мы вносим. Влияние погрешности эксперимента при этом ослабевает, но это происходит за счет того, что мы все меньше используем информацию, полученную от эксперимента. В литературе можно найти различные рекомендации по выбору α.

Довольно успешно во многих приложениях можно использовать критерий "наиболее гладкого допустимого решения", т.е. выполнять расчет при различных, все возрастающих α и остановиться на наибольшем значении α, при котором еще выполняется критерий адекватности модели (4.7).

в начало ...