| Теоретический материал | Reading materials | |||
Web-версия учебного курса "Основы математической статистики"
Раздел 4. Определение коэффициентов линейных моделей методом наименьших квадратов (МНК)После того, как выявлены основные факторы, влияющие на измеряемую величину (параметр), бывает желательно выразить зависимость параметра от факторов в аналитическом виде, это помогает представить результат работы в компактной форме. Кроме того, полученные зависимости могут быть в дальнейшем использованы в инженерных расчетах и в частности при решении задач оптимизации разрабатываемого изделия, т.к. у полученной аналитической функции могут быть найдены экстремальные точки, соответствующие максимальным (или минимальным) значениям параметра. Нахождение такой зависимости, часто помогает выяснению механизма явления или необходимо при выполнении косвенных измерений. Например, при определении температуры раскаленного тела измеряют яркость его свечения на нескольких длинах волн λ. Для абсолютно черного тела достаточно было бы измерить эту яркость на одной длине волны, но реальные тела в лучшем случае в некотором спектральном диапазоне можно считать "серыми", кроме того, абсолютные измерения яркости также требуют специального оборудования. Если считать коэффициент "серости" ε и коэффициент пропорциональности q между отсчетом фотоприемника В и яркостью тела постоянными, но неизвестными экспериментатору, то температуру Т можно найти, используя модификацию формулы Планка: B = q ε C1λ-5 exp[-C2 / (λ T)], где C1, C2 - постоянные, значение которых известно. Прологарифмировав
это выражение, его можно свести к виду
y = b1 + b2 x, b1 = ln(q ε C1), если ε или q известны, то другую величину отсюда можно найти, b2 = -1 / T, т.е. искомая величина. На первый взгляд достаточно выполнить измерения на двух длинах волн, чтобы решить систему из двух уравнений, но, как будет показано в дальнейшем, точность результата можно существенно повысить, увеличив число уравнений. Если механизм процессов, обуславливающих влияние фактора на параметр, не известен, то для отыскания аналитической формы зависимости параметра от факторов обычно пользуются эмпирическими полиномиальными моделями, т.е. предполагают заранее, что эта зависимость имеет вид полинома заданной степени, а коэффициенты полинома находят из эксперимента. Например, ищем зависимость параметра y от x1 и x2 в виде полинома второй степени: y = b1 + b2x1 + b3x2 + b4x12 + b5x22 + b6x1x2
Проделаем n > 6 опытов, в каждом j-том опыте фактор х 1 принимает определенное значение х1(j) , фактор х2 - х2(j), значение параметра y в j-том опыте - yj. В результате получим систему из n уравнений:y1 = b1 + b2x1(1) + b3x2(1) + b4[x1(1)]2 + b5[x2(1)]2 + b6x1(1)x2(1) + δ1 y2 = b1 + b2x1(2) + b3x2(2) + b4[x1(2)]2 + b5[x2(2)]2 + b6x1(2)x2(2) + δ2 * * * * * * * * * * * * * * * * * * * * * * * * * * yn = b1 + b2x1(n) + b3x2(n) + b4[x1(n)]2 + b5[x2(n)]2 + b6x1(n)x2(n) + δn Это система из n уравнений для определения шести неизвестных коэффициентов b i . Если n > 6, ее можно решить только потому, что каждое из экспериментальных значений yj отягощено случайной погрешностью δj, которую мы предполагаем нормально распределенной случайной величиной с нулевым средним и неизвестной дисперсией. Точное значение коэффициентов модели bi поэтому найти невозможно, но можно найти их оценки. Значения оценок коэффициентов bi, которые обеспечивают минимальную сумму квадратов отклонений экспериментальных значений yj от рассчитанных по модели с использованием этих оценок, называются оценками, полученными "методом наименьших квадратов" (МНК).4.1 Независимые, нормально распределенные погрешности с одинаковой дисперсией Ниже обосновывается алгоритм нахождения МНК оценок b i и оценок дисперсий bi в предположении, что все погрешности δj независимы и имеют одинаковую дисперсию, которую мы, хотя и не знаем, но можно найти ее оценку Sу2. (Методы проверки соответствующих гипотез описаны в приложении 1.)Систему уравнений запишем в матричной форме где y - столбец результатов эксперимента; b - столбец искомых коэффициентов; A - "матрица планирования" - таблица известных коэффициентов, содержащая значения уровней факторов или функции от них. Вид этой матрицы определяется, во-первых, моделью, во-вторых, конкретным выбором экспериментальных точек в области варьирования факторов.В матрице планирования столько строчек, сколько есть "экспериментальных точек", (т.е. сколько выполнено опытов при различных сочетаниях уровней факторов) и столько столбцов, сколько искомых коэффициентов модели (4.1). Результаты опытов, выполненных при одной и той же комбинации уровней факторов, как правило, усредняют и им соответствует одна строка в матрице, но можно этого не делать и представить несколько повторных опытов несколькими одинаковыми строками в матрице планирования, это не влияет на алгоритм расчетов, только при оценке адекватности модели (см. ниже) учитываются лишь различные строки матрицы планирования. Для построения алгоритма нахождения b i запишем в матричной форме условие минимизации суммы квадратов отклонений экспериментальныx значений y от рассчитанных по модели (4.1) .
S2 должно быть минимально, или dS2 /d bi = 0 для всех i. Раскроем это равенство: d (yTy - bTATy - yTAb + bTATAb) / d bi = 0, Учитывая, что равенство выполняется для всех b i, приходим к матричному равенству ATA b = ATy илиПоследнее равенство и является расчетной формулой, по которой находятся МНК оценки. Проделав несколько повторных измерений в одной экспериментальной точке, можно получить оценку Sу 2 - дисперсии погрешности y (см. формулу 1.2). Поскольку, как видно из (4.4), bi является линейной функцией всех yj, и все они предполагаются независимыми, можно, применяя свойства дисперсии ([6], глава 5), показать, что
или, преобразуя произведения элементов матриц с использованием очевидного равенства Cij2 = CjiTCij, получить окончательную формулу:
Приведенные выше общие матричные формулы позволяют, в принципе, найти коэффициенты модели при любом количестве факторов и оценить точность их определения (лишь бы число опытов было не меньше числа искомых коэффициентов). Так можно обработать и пассивный (не спланированный заранее) эксперимент, если только уровни факторов в каждом опыте известны. Однако, как видно из (4.5) погрешность определения коэффициентов модели при одной и той же точности непосредственных измерений существенно зависит от матрицы A, которая определяется как видом модели , так и числом и расположением экспериментальных точек на пространстве факторов, а это уже во власти экспериментатора. К этому мы вернемся в разделе 5 "Планирование эксперимента".Если целью эксперимента было просто определение конкретных величин, связанных с коэффициентами модели, как в рассмотренном примере измерения температуры, то задачу можно считать решенной - определена оценка искомой величины и ее "погрешность". В большинстве случаев, особенно, если модель не обоснована физическими законами следует оценить значимость коэффициентов модели, т.е. выяснить, заметен ли вклад каждого из слагаемых в значение y на фоне случайных погрешностей эксперимента. Оценка значимости коэффициентов проводится по критерию Стьюдента t, как проверка гипотезы Н 0: bi = 0. (см. разд. 3.2). Если гипотеза Н0 будет отвергнута, коэффициент bi считается значимым.Гипотеза отвергается, если
Здесь число t q берется из таблиц t-распределения (при заданном уровне значимости для проверки гипотезы Н0 и числе степеней свободы, равном числу опытов, по которым оценена Sу2, без единицы).Если в модели обнаружены незначимые коэффициенты, она должна быть упрощена и записана без них. Отбрасывание незначимых коэффициентов модели без изменения значений остальных коэффициентов допустимо лишь в том случае, если матрица ATA диагональна, тогда, как видно из формулы (4.4), вычисление bi ведется лишь с использованием элементов i-го столбца матрицы А, а другие столбцы на значение bi не влияют, т.е. все bi определяются независимо. В общем случае нужно записать новую модель без незначимых коэффициентов и все вычисления произвести заново.После того как определены все значимые коэффициенты модели остается проверить, насколько правильным было наше предположение о виде функции y = f(x). Например, если на самом деле зависимость сложнее, чем мы предположили (скажем, y = a + bx + cx 2, а мы будем искать коэффициенты модели y = b1 + b2x, то мы их найдем и они будут значимыми, но полученная модель не имеет ничего общего с действительностью).Поэтому последний этап решения задачи МНК - проверка адекватности модели. Такая проверка организуется как проверка гипотезы о том, что оценка дисперсии результата S y2, полученная при повторных опытах при одинаковых условиях и оценка Sа2, полученная из суммы квадратов отклонений результатов от расчета по модели - это оценки одной и той же дисперсии. Такая гипотеза проверяется по критерию Фишера (см. раздел 3.3):
Здесь y j - результат j-го опыта,Отношение F сравнивается с табличным значением F q, которое при выбранном уровне значимости берется при k1 = n - m и k2, равном числу опытов, по которым оценена Sу2, без единицы. Если F < Fq, (а также, если F в 4.7 меньше 1), то модель признается адекватной, т.е. отклонение экспериментальных значений от расчетов по модели можно приписать только случайным погрешностям измерений. . |
|
|||

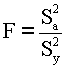 ,
где
,
где
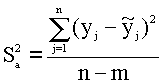 .
.