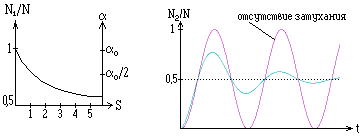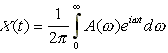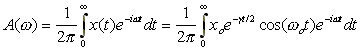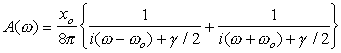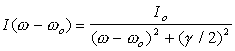Закон Бугера-Ламберта-Бэра, описывающий уменьшение интенсивности света при распространении в среде.

dI(z) = - a I(z) dz,    I(z) = I0 exp(-az)

(1)

Мощность, поглощенная единицей объема в интервале частот dw, равна

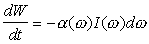(2)

где W - энергия.

Мощность, поглощенная единицей объема на переходе E_i→E_k

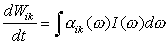(3)

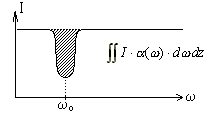
Рис.12. Интегрирование по всем частотам, дающим вклад в переход.

 

а) Если интенсивность падающего излучения мало меняется в пределах контура поглощения, то примем ее константой.

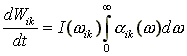(4)

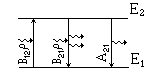
Рис.13. Виды переходов.

dP₁₂/dt - число фотонов, которое атом поглощает за 1с (вероятность поглощения за 1с)

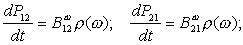
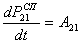
- вероятность спонтанного перехода
B₁₂, B₂₁ - коэффициенты Эйнштейна для поглощения и вынужденного излучения; r(w) - спектральная плотность энергии поля излучения.

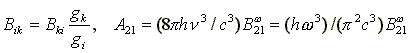
Для N_i атомов в единице объема скорость переходов равна N_iB_ik^wr(w), поглощенная мощность на переходе

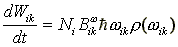(5)

Так как интенсивность плоской волны I(w) связана с плотностью энергии r(w) соотношением I(w) = c r(w), то сравнение (4) и (5) дает ∫ a_ik(w) dw = N_i B_ik^w (ħw_ik/ c). Интеграл от коэффициента поглощения не зависит от контура линии. В случае заметного заселения верхнего уровня E_k необходимо принимать во внимание влияние индуцированного излучения, которое приводит к уменьшению реального поглощения.
Связь эффективного сечения поглощения одного атома (молекулы) s_ik с коэффициентом поглощения:

aik = sik (Ni - Nkgi/gk)

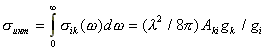
Если ширина линии определяется лишь естественной шириной, то

sинт = (l2/8p) 2pdnест gk/gi = (l/2)2 dnест gi/gk.

 

б) Если ширина линии падающего излучения уже, но сравнима с шириной контура поглощения, то выносить I(w) за интеграл в (3) нельзя и этот интеграл считают приближенными методами.
 

в) Если Dl_лаз << dl_ест (случай облучения одномодовым, одночастотным лазером), то результат будет

.

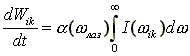Для интенсивности лазерного излучения I_л поглощенная на единице длины мощность равна dW_ik/dt = a_ikI_л. При введении профиля линии поглощения g(w-w₀), значение сечения поглощения будет

sik(w) = (ħw/c) g(w-w0) Bikw.

Зависимость сечения от частоты можно измерить, перестраивая узкое лазерное излучение по контуру линии поглощения и регистрируя ток ФЭУ (количество образовавшихся фотонов).

Измерение времен жизни и вероятности спонтанных переходов: пикосекундные и субпикосекундные лазеры.

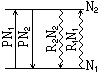
Рис.14. Схема переходов.

В достаточно слабых световых полях наблюдается линейное поглощение. Интегрирование по z выражения dI = - I s_ik (N_i - N_k g_i/g_k) dz дает закон БЛБ. При более высокой интенсивности населенности верхнего и нижнего состояний зависят от нее, и dI уже не пропорциональна I.

Пусть g₁=g₂ и существует только два изолированных уровня E₂>E₁. Полная плотность частиц - постоянна: N = N₁ + N₂. Включим дополнительно столкновительные переходы с вероятностями С₁₂ и С₂₁ и в стационарных условиях получим

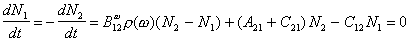(6)

или, введя R₂ и R₁,

DN = DN0 [1 + 2B12wr(w12)/(R1 + R2)]-1 = DN0 / [1+S],

(7)

где DN=N₁-N₂, а DN₀=N(R₁-R₂)/(R₁+R₂) - разность населенностей при r(w₁₂)=0. Параметр насыщения S представляет собой отношение вероятности индуцированных переходов B₁₂^wr(w₁₂) к средней вероятности релаксации R=(R₁+R₂)/2.

S = 2B12w r(w12) / (R1 + R2) = B12w r(w12) / R

(8)

Если С₁₂ и С₂₁ отсутствуют, то параметр насыщения равен отношению скоростей индуцированных (излучение + поглощение) и спонтанных переходов. При S=1 разность населенностей падает наполовину от ее ненасыщенного значения DN₀. Перепишем (7) в виде

DN = DN0 [1 + B12wI(w12) / cR]-1 = DN0 / [1 + I/Iнас]

(9)

За интенсивность насыщения принята такая величина интенсивности, которая приводит к уменьшению DN до DN₀/2. Так как a = DN s, то с увеличением интенсивности падающего излучения (I → ∞) коэффициент поглощения двухуровневой системы стремится к нулю.

a = a0 [1 + I/Iнас]-1

(10)

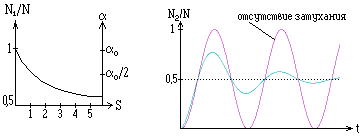
Рис.15. Графики.

В случае нестационарного воздействия, т.е. достаточно сильное поле излучения включено в момент t=0, амплитуды населенностей состояний совершают затухающие колебания и приближаются к стационарным состояниям N₁=N₂=0.5N лишь после полного затухания осцилляций на частоте Раби.

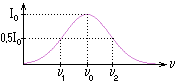
Рис.16. Профиль спектральной линии.

Ширина по полувысоте:

dl = (c/n2) dn

Естественная ширина.

Атомный электрон - затухающий осциллятор.

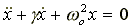(11)

x(t) - амплитуда колебаний. Начальные условия: x(0)=x₀ и x'(0)=x₀. Решение:

x(t) = x0 exp(-gt/2) [cos(wt) + (g/2w)sin(wt)].

(12)

Частота затухающих колебаний w = √w₀² - g²/4 немного меньше, чем частота w₀ (частота перехода между E_i и E_k в отсутствие затухания. Следовательно, при слабом затухании g<<w₀

x(t) = x0 exp(-gt/2) cos(w0t)

(13)

Вследствие постепенного уменьшения амплитуды x(t) испускаемое излучение уже не является монохроматическим, а обнаруживает некоторое распределение по частотам, связанное с x(t) из (3) преобразованием Фурье (см. рис.17).

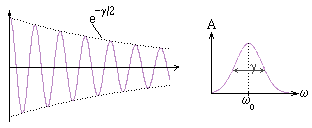
Рис.17. Естественная ширина.

X(t) - суперпозиция монохроматических колебаний e^iwt с зависящей от частоты амплитудой.

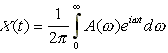	(14)
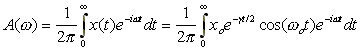	(15)

После интегрирования получаем

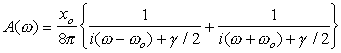(16)

Вблизи центральной частоты вторым членом можно пренебречь. Т.к. I ≈ A(w) A*(w), то

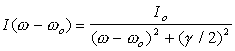(17)

Вводя нормированный профиль линии g(w-w₀) = c I(w), получим контур затухающего осциллятора - лоренцев контур.

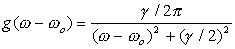(18)

Его ширина равна dw_ест = g, dn_ест = A_i / 2p = 1 / (2pt_i)

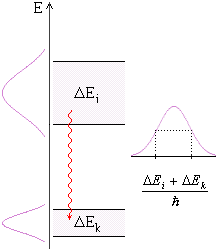
Рис.18. Пояснения.

Предыдущая формула для случая, когда затухание обусловлено распадом уровня. Это же можно получить исходя из принципа неопределенности. Энергию любого уровня можно определить с точностью DE_i ≈ ħ/t_i ; dw = (E_i - E_k)/ħ = DE/ħ = 1/t_i для стабильного конечного состояния. Если конечное состояние не основное, то dw = 1/t_i + 1/t_k . В общем случае, когда распад обоих уровней вызван не только спонтанным излучением, но также и процессами безызлучательной релаксации, профиль линии определяется суммарными константами распада g_i и g_k, каждая из которая равна g_спонт + g_безызл .

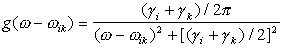(19)
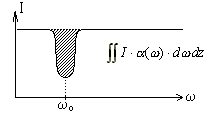
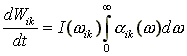
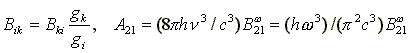
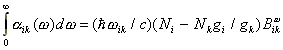
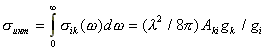
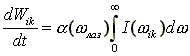