Комбинационное или рамановское рассеяние света давно используется для изучения колебательных спектров молекул и оптической ветви колебаний кристаллических решеток. Ячейка, содержащая исследуемое вещество (жидкость, газ или кристалл), облучается светом с узкой спектральной линией. Спектральный анализ рассеянного излучения обнаруживает присутствие линий, смещенных вниз по частоте на величину, равную колебательным частотам облучаемого образца. Этот тип рассеяния называется стоксовым рассеянием.

В спектре рассеянного излучения присутствуют также частоты, равные сумме частоты падающего излучения и колебательных частот вещества. Это так называемое антистоксово рассеяние, интенсивность которого на несколько порядков меньше интенсивности стоксовой компоненты.

Указанные два типа рассеяния поясняются на рис.3.

(a)		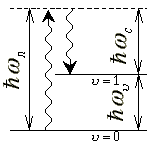Стоксово рассеяние, при котором поглощается лазерный фотон и вместе со стоксовым фотоном на частоте wc = wл - wu возникает квант колебаний молекулы (u = 1).
(b)		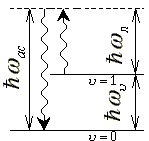Антистоксово рассеяние, при котором поглощаются лазерный фотон и колебательный квант, а испускается фотон на частоте wac = wл + wu.
(c)		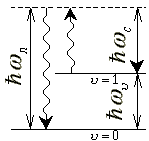Процесс поглощения фотонов частоты wc = wл - wu, стимулированный наличием лазерного излучения частоты wл.
Рис.3. Переходы при вынужденном комбинационном рассеянии.

Т.к. антистоксово излучение определяется молекулами, находящимися в возбужденном состоянии, то его интенсивность ниже интенсивности стоксова излучения на величину множителя exp (-ħw_u /kT). На рис.3 (c) представлен также обратный процесс, при котором фотон стоксовой частоты поглощается.

До недавнего времени в спектроскопии комбинационного рассеяния применялись интенсивные источники некогерентного излучения (например, ртутные лампы). В последнее время когерентные лазерные источники вытеснили ртутную лампу.

Характерные частоты колебаний атомных групп в молекулах ([2] с.370)

Частота, см-1	Колеблющаяся атомная группа	Тип соединения
445-550	S-S	Алифатические дисульфиды
510-594	C-Br	Алифатические соединения
750-850		Парапроизводные бензола
884-899		Циклопентан и монопроизводные
939-1005		Циклобутан и производные
990-1050		Бензол и одно- и трехзамещенные бензолы
≈1340		Ароматические соединения
≈1380		Нафталин и производные
≈1630	C=N	Ароматические соединения
1654-1670	C=N	Алифатические соединения
1974-2260	C≡C	Алифатические соединения
2150-2245	C≡N	Нитрилы
4160	H-H	H2

Характерно, что частоты мало меняются от соединения к соединению.

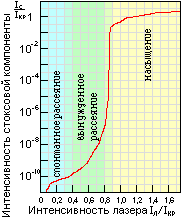Рис.4. Зависимость интенсивности генерации стоксовой компоненты от интенсивности накачки лазера ([2] c.380.)

Если среду, способную к комбинационному рассеянию, поместить в оптический резонатор, то при наличии поля лазерной накачки усиление стоксовой компоненты способно скомпенсировать потери, и на частоте w_c возникает генерация. Генерация при ВКР представляет собой практический способ преобразования излучения импульсных лазеров (например, лазера на неодимовом стекле) в когерентное излучение, сдвинутое по частоте на колебательную частоту вещества.

Эксперименты по исследованию влияния интенсивности лазерной накачки на интенсивность стоксовой компоненты показали, что по достижении некоторой критической интенсивности накачки интенсивность стоксовой компоненты резко возрастает, а затем идет насыщение (см. рис.4).

В экспериментах по ВКР было обнаружено, что выходное излучение содержит несколько стоксовых (w_л - w_u ), (w_л - 2w_u ), ... и антистоксовых (w_л + w_u ), (w_л + 2w_u ), ... компонент. Из рис. 3 видно, что процесс излучения стоксовой компоненты приводит к увеличению населенности колебательного уровня (u=1), поэтому становится возможным излучение на антистоксовой частоте. Стоксова (w_c) и антистоксова (w_ас) компоненты могут, в свою очередь, служить исходным излучением, генерирующим частоты w_с - w_u = w_л - 2w_u и w_ас + w_u = w_л + 2w_u. Аналогично можно объяснить появление комбинационных частот более высоких порядков.

Чтобы пояснить основные особенности возникновения ВКР, получим условие усиления или генерации на первой стоксовой частоте w_с = w_л - w_u, т.к. первоначально может усиливаться только эта компонента. Для возникновения других спектральных компонент требуется либо наличие молекул в возбужденном состоянии, либо присутствие стоксовой компоненты первого порядка.

Для анализа используется такая модель: рассеивающая среда состоит из N независимых осцилляторов (т.е. ансамбль осцилляторов не поддерживает волновое движение с отличной от нуля групповой скоростью), каждый характеризуется своим положением z (одномерный случай Δ/Δx=Δ/Δy=0) и нормальной колебательной координатой X(z,t). Уравнение движения для осциллятора имеет вид

(1)

где Г - постоянная затухания, выбранная так, что наблюдаемая ширина линии спонтанного комбинационного рассеяния равна Dn=^G/_2p; w_u - резонансная частота колебаний молекулы в отсутствие затухания; m - масса; F(z,t) - возбуждающая сила.

Возбуждающую силу можно получить, рассматривая электромагнитную энергию в молекулярной среде. Плотность энергии, запасенной в электрическом поле E=¹/₂eE² при использовании равенства

e = e0 (1 + Na) = e0 {1 + N [a0 + (Δa/ΔX)0 X]}

(2)

может быть записана в виде

E=1/2 e0 {1 + N [a0 + (Δa/ΔX)0 X]} E2

(3)

Сила, действующая на единицу объема поляризуемой среды, равна Δe/ΔX, откуда делением на N получаем силу, действующую на один осциллятор.

F(z,t)=1/2 e0 (Δa/ΔX)0 <E(z,t)>2

(4)

<E(z,t)> означает усреднение за несколько колебаний, предпринимаемое потому, что молекула неспособна реагировать на эти колебания. Из (4) видно, что при отличной от нуля дифференциальной поляризуемости (Δa/ΔX)₀ колебания молекул могут возбуждаться электрическим полем.

Дальнейшая задача - показать, как колебания молекул воздействуют на электромагнитное поле. В соответствии с (2) колебания молекул с частотой w_u вызывают модуляцию диэлектрической проницаемости с той же частотой. Это приводит к фазовой модуляции поля излучения (появляются боковые составляющие, смещенные на w_u друг от друга). Т.е. происходит обмен энергией между электромагнитными полями различных частот., разделенных интервалами, кратными w_u.

Полное поле является суммой лазерного (w₂) и стоксова (w₁) полей:

E(z,t) = 1/2 E1(z) exp iw1t + 1/2 E2(z) exp iw2t + к.с.	(5)
<E(z,t)>2 = 1/4 E2(z) E1*(z) exp i(w2-w1)t + к.с.	(6)
(6) → (4) → (1)
	(7)

Здесь использованы соотношения Δ/Δt=iw и

X(z,t) = 1/2 X(z) exp iwt + к.с.

(8)

Из (7) следует, что на частоте w=w₂-w₁ молекулярные колебания имеют комплексную амплитуду

(9)

Поляризация, наведенная полем частоты w₁, имеет вид

P = e0 N a(z,t) E(z,t) = e0 N [a0 + (Δa/ΔX)0 X(z,t)] E(z,t).

(10)

Используя (5), (9) и (10) для нелинейная поляризации (второй член поляризации, пропорциональный X E) получаем:

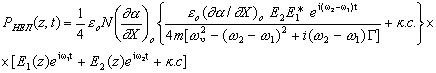(11)

Примечание:

Осуществив умножение в формуле (11) (см. тж. примечание), получим составляющие поляризации, осциллирующие с частотами w₁, w₂, 2w₁-w₂ и 2w₂-w₁. Рассмотрим сначала составляющую нелинейной поляризации, имеющую частоту w₁:

Pнелw1(z,t) = 1/2 Pнелw1(z) exp iw1t + к.с.,

(12)

где

(13)

Коэффициент пропорциональности между полем и поляризацией представляет собой восприимчивость. Нелинейная комбинационная восприимчивость подобно линейной восприимчивости имеет лоренцеву форму линии.

Форма линии стоксова рассеяния имеет вид

(13a)

Антистоксово излучение на частоте w₃ = w₂ + w_u является результатом комбинационного рассеяния света молекулой, находящейся в возбужденном колебательном состоянии (u=1). При классическом подходе к задаче мы должны найти поляризацию на w₃, наведенную электрическим полем:

E(z,t) = 1/2 [E1(z) exp iw1t + E2(z) exp iw2t + E3(z) exp iw3t + к.с.],

(14)

где w₃ - w₂ = w₂ - w₁.

В выражении для поляризации по аналогии с (11) найдем член, соответствующий возбуждению молекулярных колебаний силой, пропорциональной E₃ E₂^*. Из (13) заменой частот и индексов у E получим

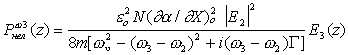(15)

Важно, что мнимые части (13) и (15) имеют разные знаки, поэтому

Существует, однако, еще одна компонента поляризации на частоте w₂:

Pнелw3(z) ~ E2 E2 E*1 exp [i(2w2-w1)t]

(16)

Она не содержит E₃ и может рассматриваться как верхняя боковая частота [w₂ + (w₂ - w₁)] в спектре модулированных колебаний диэлектрической проницаемости с несущей w₂ и модулирующей w₂ - w₁ частотами. Эта компонента является источником излучения с частотой w₃.

Если дополнить (16) пространственной зависимостью поляризации, то

Pнелw3(z) ~ E2 E2 E*1 exp [-i(2k2-k1)r]

(17)

Этому члену соответствует поле E₃exp(-ik₃r), причем

k3 = 2 k2 - k1

(18)

Следовательно, антистоксова волна может излучаться только в направлениях, удовлетворяющих условию (18). См. рис.5. А так как |k_i| = w_i n_i / c, то антистоксова компонента распространяется в направлениях, составляющих коническую поверхность с половинным углом b при вершине и осью лазерного луча.

Реальная ситуация сложнее. Помимо наличия стоксовых и антистоксовых компонент высоких порядков, имеет место отклонение от направлений, рассчитанных по формуле (18) из-за эффекта самофокусировки.

Рис.5. Диаграмма для определения направления распространения антистоксова излучения.

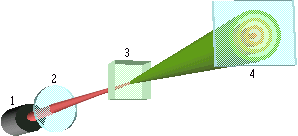Рис.6. Схема эксперимента по изучению комбинационного рассеяния. 1 - рубиновый лазер; 2 - линза; 3 - ячейка с бензолом; 4 - экран Цвета показаны условно.

Выше уже упоминалось, что ВКР в среде наступает только при превышении некоторого порога интенсивности электрического поля. Однако измеренная пороговая интенсивность часто оказывается ниже ожидаемой. Расхождения между теорией и экспериментом могут быть весьма значительными: в некоторых жидкостях соответствующие пороги отличаются в сотни и более раз, что обусловлено явлением самофокусировки. В таком случае диаметр пучка по мере распространения в среде уменьшается и на некотором расстоянии пучок собирается в "фокусе". В фокальной области плотности мощности лазерного излучения очень велики и могут привести к разрушению материала. Это явление имеет непосредственное отношение к импульсным лазерам с очень высокой мощностью излучения, поскольку разрушению может подвергаться и активный элемент лазера.

В первой лекции были выведены зависимости c(w,E₀) и c(3w,E₀) (формулы (23)), на основе которых можно записать:

eобщ = 1 + c + bE2 ,

(19)

тогда

nобщ = √eобщ ≈ n + n2 E2 , где n2 = b / 2n

(20)

Если n₂>0, то в местах большой напряженности поля - показатель преломления больше. Т.е. в нелинейном материале сам пучок формирует положительную линзу. Это так называемая крупномасштабная самофокусировка. Существует также мелкомасштабная самофокусировка, обусловленная нарастанием возмущений в пучке в поле мощной световой волны.

На рисунках показано применение ВКР.

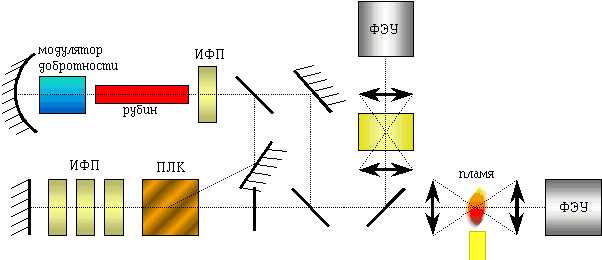Рис.7a. КАРС спектроскопия.

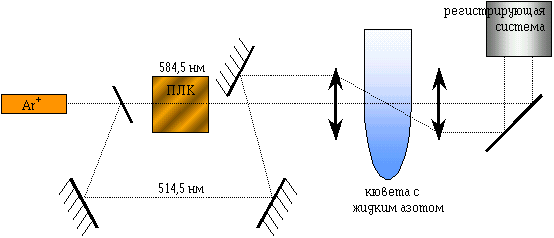Рис.7b. Многопроходные кюветы.