НЕЛИНЕЙНАЯ ОПТИКА |
Появление мощных источников когерентного светового излучения (лазеров) привело к возникновению нового направления исследований, связанного с изучением взаимодействия мощных когерентных потоков электромагнитного излучения с веществом, получившего название "Нелинейная оптика".
Оптические эффекты, характер которых зависит от интенсивности излучения, называют нелинейными, а область оптики, изучающая нелинейные оптические эффекты (оптика мощных световых потоков) - нелинейной оптикой.
До появления лазеров число нелинейных оптических эффектов можно было перечислить
по пальцам. Существовавшие до лазеров источники давали световые волны слишком малой
интенсивности и, как следствие, этого большинство наблюдаемых оптических эффектов не
зависело от интенсивностей волн. Только после появления лазеров - источников света,
позволяющих получить световые волны с напряженностями полей
Любой электромагнитный процесс в среде описывается уравнениями Максвелла:
| (1) |
Однако этих уравнений недостаточно для решения электромагнитной задачи, необходимы материальные
уравнения, устанавливающие дополнительные связи между указанными векторами.
| D=e0E+P', B=m0H+M', j=sE | (2) |
В изотропном случае макроскопическая поляризация среды зависит от напряженности
электрического поля E. Коэффициентом пропорциональности в такой зависимости
является диэлектрическая восприимчивость среды
| P'=e0 c(E) E → (2) : D=(1+c(E)) e0 E = e(E) E | (3) |
В слабых полях восприимчивость среды (и диэл. проницаемость) - константа, не зависящая
от напряженности электрического поля. Следовательно, реакция среды на внешнее поле - линейная:
| P'=e0 c0 E, D=(1+c0) e0 E = e0 e E, e=1+c0 | (3a) |
Нелинейные эффекты проявляются лишь тогда, когда поля достаточно сильны и величины c
и e уже нельзя считать не зависимыми от напряженности поля. Чтобы проиллюстрировать
появление нелинейной зависимости величин c и e, вычислим их в рамках простой
классической задачи. Рассмотрим газ, состоящий из атомов (два точечных заряда: ядро и электрон)
без постоянного электрического дипольного момента. В отсутствие внешнего поля положение точечных
зарядов совпадает. Поместим его в постоянное электрическое поле. Заряды в каждом атоме сместятся
на некоторое расстояние. Для простоты будем считать, что смещение электрона совпадает
с направлением внешнего электрического поля. Тогда можно не учитывать векторного характера
величин, входящих в задачу, и оперировать скалярами. Таким образом, атомы приобретут дипольный
момент
Если было
| P' = N d = N e r | (4) |
На электрон действуют две силы: одна - действие электрического поля -
| e E = k r + q r3; | (5) |
Из (4) выражаем
| (6) |
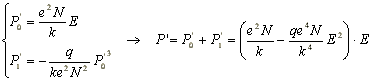 |
(7) |
| (7a) |
Т.е. восприимчивость является нелинейной функцией напряженности поля. Если же поле
достаточно слабое (значительно меньше внутриатомного), то вторым членом можно пренебречь
(это означает, что смещение
До этого мы рассматривали случай изотропной среды. Когда среда анизотропна,
восприимчивость и проницаемость вместо скаляров становятся тензорами второго ранга,
а связь между векторами P', D, E имеет вид
| (8) |
Для декартовой системы координат:
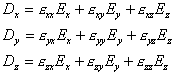 |
(8a) |
Зная параметры внешнего электрического поля и тензор восприимчивости для данного кристалла, обычно определяемый экспериментальными методами, можно всегда рассчитать его поляризацию.
Рассмотрим поляризацию диэлектрика в высокочастотном поле на той же
простейшей модели газа. Поскольку напряженность электрического поля теперь зависит
от времени, необходимо решать динамическую, а не статическую задачу для движения электрона.
Уравнение движения электрона запишется в виде
| (9) |
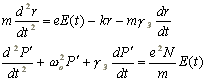 |
(10) |
Пусть поле меняется по гармоническому закону
|
(w02 - w2) P0
(cos wt cos j - sin wt sin j) - - gзwP0 (cos wt sin j + sin wt cos j) = e²N/m E0 cos wt |
(10a) |
Приравняем по отдельности члены при
|
- (w02 - w2) sin j -
gзw cos j = 0 (w02 - w2) P0 cos j - gзwP0 sin j = e2 N E0 / m |
(11) |
| (12) |
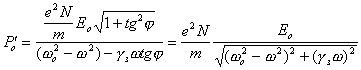 |
(11a) |
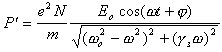 |
(13) |
В этом случае фаза поляризации близка к нулю (см. (12)). Тогда поляризация
| (13a) |
т.е. восприимчивость зависит от частоты.
До сих пор предполагалось, что на электрон действует поле малой напряженности.
Мы брали
| (14) | |
| (15) |
Будем, как и раньше считать, что поле
| (16) | |
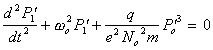 |
(17) |
| (18) |
| E3(t) = 1/4 E03 (3 cos wt + cos 3wt) | (19) |
Уравнение (18) - это уравнение гармонического осциллятора, на который действует
внешняя сила (правая часть уравнения), состоящая из двух компонент,
одна из которых меняется с частотой w, а другая - с частотой
3w. Поэтому решение будем искать в виде
| (20) | |
| (21) |
| P'= P'0 + P'1 = c(w,E0) E0 cos wt + c(3w,E0) E0 cos 3wt | (22) |
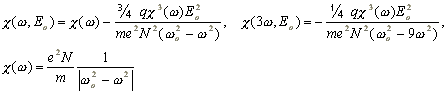 |
(23) |
Поляризация в сильном световом поле является функцией не только частоты падающего излучения, но и его третьей гармоники. Известно, что заряд, совершающий гармоническое колебание с некоторой частотой, излучает монохроматическую электромагнитную волну той же частоты. Поэтому в рассмотренной задаче появляются две волны: одна с частотой w, другая - с частотой 3w.
Таким образом, в рамках простейшей модели мы показали, каким образом из-за нелинейных свойств среды в сильном световом поле возникают высшие гармоники.
|
Web-дизайн:
Соловьев А. Последние изменения 01.06.2000. |
[2-я часть] [Содержание] [Методические пособия] |