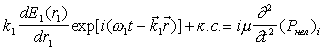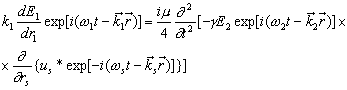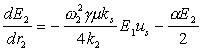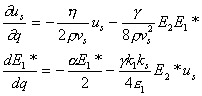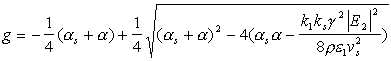Спонтанное рассеяние света на тепловых акустических волнах было рассмотрено Бриллюэном
еще в 1922 г. (Одновременно с Бриллюэном и независимо от него рассеяние света в твердых телах
теоретически исследовал Л.И.Мандельштам). Вынужденное рассеяние, когда акустическая волна,
рассеивающая свет, сама возбуждается этим светом, было открыто в 1964 г. При пропускании
через кристалл (сапфира или кварца в первых экспериментах) мощного лазерного излучения частоты
w2 в кристалле возбуждалась акустическая волна с частотой
ws и одновременно генерировалось оптическое излучение
частоты w2-ws.
И акустический, и рассеянный оптический лучи испускались в строго определенных направлениях
и возникали только при условии, что мощность лазера превышала определенное пороговое значение.
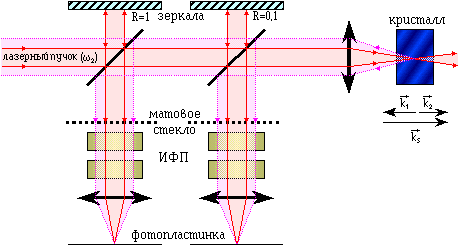
Рис.8. Схема первого эксперимента по наблюдению ВРМБ.
|
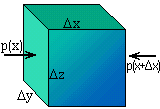
Рис.9. Элементарный объем единичного сечения (Dz Dy = 1)
и длины Dx.
|
Переменное электрическое поле вызывает в результате электрострикции переменную деформацию
в жидкости или кристалле, возбуждая таким образом акустические волны. Акустическая волна
модулирует диэлектрическую проницаемость среды, что может привести к обмену энергией между
электромагнитными волнами, частоты которых отличаются на величину, равную частоте акустической
волны. Это явление аналогично ВКР, только роль молекулярных колебаний играет акустическая волна.
Для вывода уравнений распространения звуковой волны рассмотрим элементарный объем
dxdydz внутри жидкости, на который действует электрическое поле (рис.9).
Пусть смещение точки от равновесного положения - u(x,t),
так что одномерная деформация равна Δu/Δx.
Введем феноменологическую постоянную g, характеризующую изменение диэлектрической
проницаемости под влиянием деформации:
При наличии деформаций плотность запасенной электрической энергии изменяется на величину
- 1/2 g (Δu/Δx) E2.
Изменение запасенной энергии, связанное с деформацией среды, означает существование давления:
Полная электрострикционная сила, действующая на единичный объем в направлении
оси X равняется
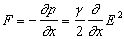 , , |
(2a) |
а уравнение движения для
u(x,t) записывается в виде
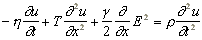 , , |
(3) |
Примечание:
T = (1/r) (dr/dp)
|
где
h - постоянная затухания, учитывающая акустические потери;
Т и
r - соответственно упругая постоянная (объемный модуль) и плотность среды.
Предположим, что акустическое и оба электрических поля представляют собой плоские волны,
бегущие в произвольных направлениях:
E1(r,t) = 1/2 E1(r1)
exp[i (w1t - k1r)] +
к.с.,
E2(r,t) = 1/2 E2(r2)
exp[i (w2t - k2r)] +
к.с.,
u(r,t) = 1/2 us(rs)
exp[i (wst - ksr)] +
к.с.,
|
(4) |
где
r1, r2, rs - расстояния с учетом знака
вдоль направлений распространения
k1,
k2,
ks, так что
ri = (ki•ri)/ki.
Дифференцируя последнее уравнение в (4) в предположении
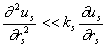 ,
ks2 us, получим
,
ks2 us, получим
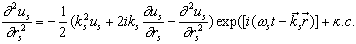 |
(4a) |
Заменив в (3) x на rs, получим
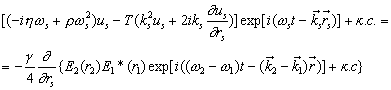 |
(5) |
Из (5) следует, что ws = w2 - w1,
ks = k2 - k1
и правая часть (5) преобразуется к виду
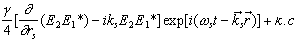 , , |
(6) |
а волновое уравнение (5) в целом принимает вид
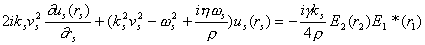 |
(7) |
где
vs - скорость распространения акустических волн
(vs2 = T/r).
Уравнение (7) справедливо при условии, что
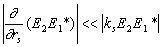 .
.
Уравнение для электромагнитных волн.
Волновое уравнение:
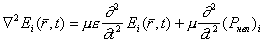 , , |
(8) |
где (Pнел)i - компонента нелинейной поляризации,
возбуждающая поле Ei(r,t).
Используя первое равенство из (4) получаем
|
С2E1(r,t) = - 1/2
[k12E1(r1) +
2ik1СE1(r1) -
С2E1(r1)]
exp[i (w1t - k1r)] +
к.с.
|
(9) |
Подставим его в (8) (i=1), пренебрежем членом
С2E1(r1) и, вспомнив, что
k1 СE1(r1) =
k1 (dE1/dr1), придем к уравнению
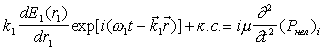 |
(10) |
Нелинейная поляризация в (10) - это дополнительная поляризация, вызванная акустической
волной, т.е. (Pнел)i = (de)E, или с учетом (1)
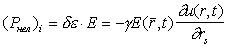 |
(11) |
Согласно (4) произведение E (du/drs) содержит члены,
колеблющиеся с частотами (±ws±w1) и
(±ws±w2). Однако лишь те, для которых
±(w2 - ws) = ±w1,
действуют как синхронные источники, так что уравнение (10) можно записать в виде
или с учетом (6)
При
|dus/drs| << |ksus|
волновое уравнение принимает вид
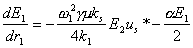 |
(12) |
причем диссипативный член
-(aE1/2) добавлен для учета потерь
в среде на частоте
w1, которыми до сих пор пренебрегали.
Также выводится уравнение
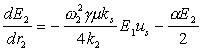 |
(13) |
для волны с частотой
w2 = w1 + ws.
Соотношения (7), (12) и (13) образуют замкнутую систему уравнений относительно
амплитуд акустического us(rs) и электромагнитных полей
E1(r1) и E2(r2).
Вынужденное рассеяние Мандельштама-Бриллюэна.
В этом случае интенсивное поле с частотой w2 вызывает
одновременную генерацию электромагнитной волны с частотой w1 и
акустической волны с частотой ws = w2 - w1.
Анализ упрощается, когда генерируемые волны намного менее интенсивные, чем лазерное излучение.
Тогда E2(r2) = const и рассматриваем только (7) и (12).
В первом из них положим ws = ks vs,
т.е. примем для акустической волны тот же закон дисперсии, что и в случае свободного
распространения в среде без потерь. Тогда
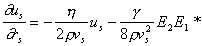 , , |
(14) |
а уравнениее (12) перепишется в виде
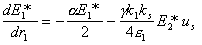 |
(15) |
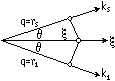
Рис.10. Соответствие между координатами.
|
Трудность, обусловленная наличием двух переменных (r1 и
rs) в связанных уравнениях (14) и (15), может быть устранена
путем перехода к координате x, измеренной вдоль биссектрисы угла,
как показано на рис.10. Используя соотношение
rs = r1 = x cos q = q,
можно перейти от (14) и (15) к
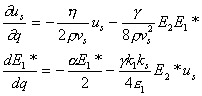 |
(16) |
Эти уравнения описывают нарастание (или затухание) акустического смещения
us и электрического поля
E1
вдоль любого из двух направлений распространения, которому сопоставляется координата q.
Предположим нарастание экспоненциальным
|
us(q) = us0 eg q,
E1*(q) = (E10)* eg q
|
(17) |
Подставим (17) в (16) и решим характеристическое уравнение. Решение имеет вид
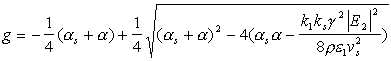 |
(18) |
где
as = - h/rvs -
акустическая постоянная затухания. Показатель усиления g растет
при увеличении акустической частоты
ws.
Поскольку
ws << w2,
то
w2 ≈ w1 и для изотропной
среды
k2 ≈ k1.
Векторное соотношение (6) оказывается таким же как и для брэгговского рассеяния, следовательно,
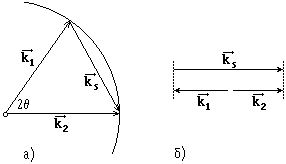
Рис.11. Соотношение между векторами k2, k1 и
ks при ВРМБ в изотропной среде:
а) для произвольного угла q;
б) в случае обратного рассеяния (q≈p/2)
|
Усиление максимально в случае обратного рассеяния
(q=p/2):
ks = 2k2, а акустическая волна имеет частоту
|
(ws)max = 2 w2 vs
n2 / c.
|
(20) |
Когда
g>0, тепловые акустические волны, распространяющиеся вдоль
ks, и световые волны, распространяющиеся вдоль
k1
и имеющие частоту
w1, будут одновременно усиливаться по закону (17).
Это вызовет соответствующее нарастание мощностей волн, распространяющихся вдоль этих направлений.
Условие усиление для ВРМБ выполняется при
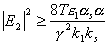 |
(21) |
Если выразить акустическую и оптическую постоянные затухания через характерные длины
затухания Ls = 2/as и
L1 = 2/a, (т.е. расстояния, на которых амплитуды полей
в обычных условиях спадают в е раз), то выражение для пороговой накачки примет вид
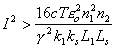 |
(22) |
Пример: ВРМБ для кварца.
Т = 5•1010 Н/м2 -
типичное значение модуля упругости твердых тел,
g ≈ e0 ~ 10-11 Ф/м -
типичное значение коэффициента электрострикции,
l2 ≈ l1 = 1 мкм,
L1 = 1 м,
k1L1 = (2pL1/l1) =
2p•106,
ws ≈ 2w2 (vsn/c)
≈ 12p•109 с-1,
при
vs = 3•103 м/с,
Ls = 10-3 м -
типичное значение для кварца и сапфира.
Оценка пороговой мощности дает:
Iпор ≈ 1011 Вт/см2.
На этот эффект очень сильно влияет самофокусировка.
Интересен случай, когда k1•k2<0.
Он имеет место, когда угол 2q между падающим (w2)
и рассеянным (w1) световыми лучами превышает p/2.
Тогда скорость нарастания рассеянной волны зависит от значения E1
в точках, расположенных вдоль направления k1 перед рассматриваемым
волновым фронтом. Такая обратная связь обеспечивается акустической волной в силу ее
противоположного направления распространения. Аналогичным образом рассеянная световая волна
частоты w1 обеспечивает обратную связь для акустической волны.


![]() ,
,
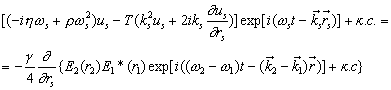
![]() .
.