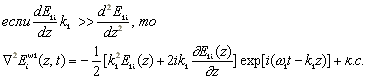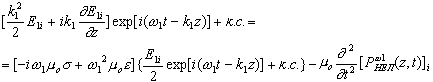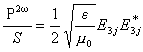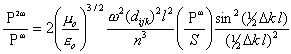Рассмотрение взаимодействия электромагнитных полей начнем с записи уравнения Максвелла, выделив в явном виде поляризацию P:

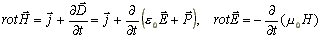(4)

Представив поляризацию в виде суммы линейного и нелинейного членов, перепишем первое уравнение.

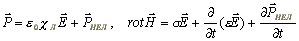(5)

Примечание: rot rot E = grad div E - С2E

Возьмем ротор от обеих частей второго уравнения (4) и подставим rot H из (5) (см. тж. примечание), учитывая, что div E=0:

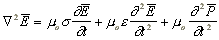(6)

Дальнейший анализ проведем для одномерного случая (Δ/Δx=Δ/Δy=0). За направление распространения берем ось Z. Ограничимся рассмотрением взаимодействия колебаний трех частот и соответствующие поля возьмем в виде бегущих плоских волн:

Eiw1(z,t) = 1/2[E1i(z) exp i(w1t-k1z) + к.с.], Ekw2(z,t) = 1/2[E2k(z) exp i(w2t-k2z) + к.с.], Ejw3(z,t) = 1/2[E3j(z) exp i(w3t-k3z) + к.с.],

(7)

где ijk - декартовы координаты. Заметим, что при P_нел=0 решение уравнения (6) дается выражениями (7) с амплитудами, не зависящими от z. В качестве примера запишем i-компоненту нелинейной поляризации на частоте w₁=w₃-w₂. Согласно (3) и (7) она имеет вид

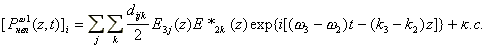(7a)

Вернемся к уравнению (6). В одномерном случае

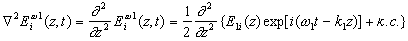(8)

Дифференцируем и полагаем, что изменение комплексных амплитуд полей достаточно медленное, т.е.

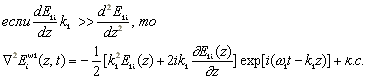(9)

Аналогичные выражения можно вывести для С²E_j^w3(z,t) и С²E_k^w2(z,t). Подставляя (9) в (6) и используя соотношение Δ/Δt=iw₁ получим волновое уравнение для E_i^w1(z,t):

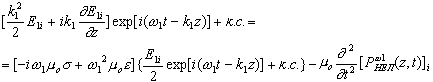(10)

Предполагаем, что при взаимодействии конечного числа полей уравнение (6) должно удовлетворяться по отдельности для компонент с различными частотами. Поставив (7а) и заметив, что w₁²m₀e=k₁², получим

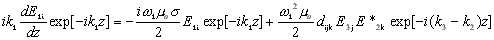(11)

или (считая s функцией частоты)

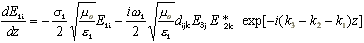(11a)

и аналогично

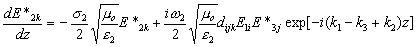(11b)

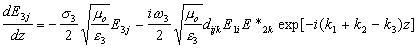(11c)

Эти уравнения мы применим в дальнейшем при рассмотрении ряда конкретных случаев.

Первый эксперимент по генерации второй гармоники света был выполнен Франкеном в 1961 году. Луч рубинового лазера с l = 694,3 нм фокусировался на поверхность пластины из кристаллического кварца. Выходящее излучение анализировалось спектрометром. Было найдено, что в нем содержится компонента с удвоенной частотой (т.е. с l = 347,15 нм). Эффективность преобразования в первых экспериментах была порядка 10^-8. Использование более эффективных материалов, увеличение мощности лазера, обеспечение условий фазового синхронизма позволили в последние годы довести коэффициент преобразования почти до единицы.

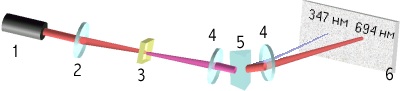
Рис.1. Схема первых экспериментов по ГВГ. 1 - рубиновый лазер, 2 - фокусирующая линза, 3 - кварцевая пластинка, 4 - коллиматорные линзы, 5 - призма, 6 - фотопластинка (экран). Цвета показаны условно.

Применим уравнения (11a-11c) для рассмотрения ГВГ. Это частный случай взаимодействия полей трех частот, когда две частоты w₁ и w₂ одинаковы, а w₃ = 2 w₁. Следовательно, необходимо анализировать только два уравнения: первое (или второе) и последнее. В целях упрощения будем считать, что потери мощности входного луча (w₁) за счет преобразования во вторую гармонику малы, т.е. dE_1i/dz ≈ 0. Следовательно, можно рассматривать только последнее уравнение (11c). Если среда прозрачна на частоте w₃, то s₃=0 и

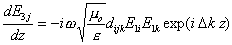(12)

где w = w₁ = ¹/₂ w₃,  Dk = k₃^(j) - k₁⁽ⁱ⁾ - k₁^(k),  а k₁⁽ⁱ⁾ - волновое число волны с частотой w₁, поляризованной по оси i. Если E_3j(0) = 0, т.е вторая гармоника на входе отсутствует, и кристалл имеет длину l, решением (12) будет

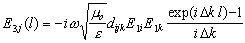(13)

или

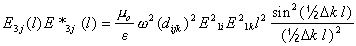(14)

где e≡e₃. Чтобы получить выражение для мощности второй гармоники P^2w на выходе, воспользуемся соотношением

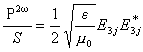(15)

где S - площадь поперечного сечения пучка. Приняв e₁≈e₃≈e₀n² приходим к коэффициенту преобразования

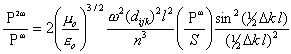(16)

Из (16) следует, что предпосылкой для эффективной ГВГ является выполнение условия Dk = 0, или, поскольку w₃ = 2 w, а w₁ = w₂ = w,

Dk = k2w - 2 kw = 0 →  k2w = 2 kw

(17)

Если Dk ≠ 0, то волна удвоенной частоты, генерируемая в некоторой плоскости (z₁), дойдя до другой плоскости (z₂), окажется не в фазе с волной удвоенной частоты, генерируемой в этой плоскости. Результат интерференции таких волн представлен в (16) множителем (¹/₂ Dk l)^-2 sin²(¹/₂ Dk l). Два соседних максимума этой интерференции удалены на расстояние, называемое "когерентной длиной":

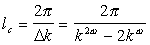(18)

Она является в сущности максимальной длиной кристалла, которую можно использовать для ГВГ. Показатель преломления, как правило, растет с увеличением частоты, так что

Dk = k2w - 2 kw = (2 w /c)(n2w - nw)

(19)

Здесь использовано k=wn/c. Когерентная длина выражается формулой

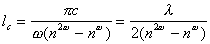(20)

в которой l - длина волны падающего света.

Способ, который широко применяется для обеспечения условий фазового синхронизма, заключается в использовании анизотропных кристаллов, обладающих естественным двулучепреломлением. Используя связь k^w = w √me₀ n^w, вместо условия (17) получим условие n^2w = n^w, т.е. коэффициенты преломления на основной частоте и на удвоенной должны совпадать. В материалах с нормальной дисперсией показатель преломления обыкновенной и необыкновенной волн, распространяющихся в данном направлении, растет с частотой. Т.е. удовлетворить условию равенства коэффициентов преломления невозможно, если волны частот w и 2w принадлежат одному типу (обыкновенные или необыкновенные). Однако фазовый синхронизм может осуществляться благодаря использованию волн разных типов.

В качестве примера рассмотрим зависимость показателя преломления необыкновенной волны в одноосном кристалле от угла q между направлением распространения и оптической осью (осью Z) кристалла. Эта зависимость имеет вид

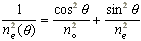(21)

Если n_e^2w < n_o^w, то существует угол q_синх, при котором n_e^2w(q_синх) = n_o^w. Таким образом, если волна частоты w распространяется под углом q_синх к оси и имеет поляризацию, отвечающую обыкновенному лучу, то волна удвоенной частоты, возбуждаясь в том же направлении, будут обладать поляризацией необыкновенного луча. (См. рис.2).

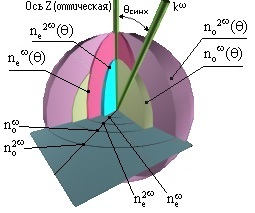
Рис.2. Поверхности показателей преломления для обыкновенного и необыкновенного лучей в отрицательном одноосном кристалле.

Угол q определяется пересечением сферы, представляющей собой поверхность показателей преломления для обыкновенного луча частоты w (желтая сфера) с эллипсоидом показателей преломления необыкновенного луча частоты 2w (розовый эллипсоид). В случае отрицательного одноосного кристалла (n_e^w < n_o^w), угол, удовлетворяющий условию n_e^2w(q_синх) = n_o^w, определяется так

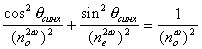(22)

откуда

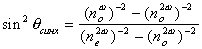(23)