Web-версия учебного курса "Теория вероятностей"
Раздел 9. Центральная предельная теорема и ее следствия
Нормальное распределение -наиболее распространенное в природе распределение непрерывных величин. Математическим обоснованием этого факта служит центральная предельная теорема:
Сумма большого числа как угодно распределенных независимых случайных величин распределена асимптотически нормально, если только слагаемые вносят равномерно малый вклад в сумму.
Это значит, что чем больше независимых слагаемых в сумме, тем ближе закон ее распределения к нормальному. Вместо суммы часто рассматривают среднее арифметическое большого числа случайных величин, оно отличается от суммы только множителем (1/n) , поэтому его распределение также стремится к нормальному с ростом числа n суммируемых величин. Поскольку случайные величины, с которыми мы сталкиваемся, например, при измерениях, есть результат действия множества независимых факторов, понятно, почему измеряемые значения, как правило, распределены нормально.
Следствием центральной предельной теоремы является широко применяемая при решении задач теорема Муавра-Лапласа:
Если производится серия n независимых испытаний, в каждом из которых некоторое событие происходит с вероятностью р,
то закон распределения величины 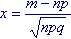 , ,
где m - число появлений события в n испытаниях, а q = 1 - p , стремится к нормальному с матожиданием 0 и дисперсией 1 при n, стремящемся к бесконечности.
Поскольку плотность нормального распределения с матожиданием 0 и дисперсией 1 как функция х, а также значение интеграла от этой плотности в пределах от 0 до z как функция z табулированы во всех учебниках и задачниках по теории вероятностей, то легко найти вероятность попадания х, а следовательно и m при известных n, p в любой интервал.
|