Web-версия учебного курса "Теория вероятностей"
Раздел 5. Случайные величины и функции распределения
Строго понятие "случайная величина" определяется так:
Пусть имеется пространство элементарных событий U, на нем построено поле событий и для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному событию gi из U сопоставим число ξi. Потребуем, чтобы для любого х (-∞ < x < +∞) множество А тех g, для которых ξ < x , принадлежало полю событий, т.е. для него определена вероятность Р{ξ < x} = P(A) = F(x). Тогда ξ называется случайной величиной, а F(x) - ее функцией распределения.
Проще можно сказать, что случайная величина - это величина, значение которой зависит от случая, если для всех х известна функция распределения F(x), т.е. вероятность того, что это значение меньше х.
В строгом определении задание пространства элементарных событий означает по существу задание условий, в которых возникают те или иные значения случайной величины, а если эти условия заданы, то тем самым определена и F(x). Например, нельзя сказать, что "температура - случайная величина". Но "температура воздуха, измеряемая на данной метеостанции в случайный момент времени в течение года" - случайная величина, "температура воздуха в случайно выбранной точке земного шара 1 января 2001г. в 12.00 по Московскому времени" - другая случайная величина.
Свойства функции распределения:
- F(-∞) = 0
- F(+∞) = 1
- F(x) - не убывающая функция х
Случайные величины могут быть непрерывными, т.е. принимать любые значения в некотором интервале (например, упомянутые выше температуры). У них F(x) - непрерывная функция.
Случайные величины могут быть дискретными т.е. принимать только конечное или счетное множество определенных значений (например, число очков при бросании игральной кости; число телефонных звонков, поступающих конкретному абоненту в течение суток). У таких величин F(x) имеет разрывы в точках, соответствующих принимаемым значениям. Такие величины удобнее характеризовать указанием возможных значений и их вероятностей.
| Пример 1: число очков при бросании кости |
| Значения хi: | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятности р(хi) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Функция распределения:
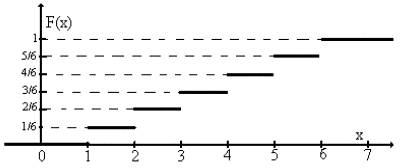
Рисунок 5.1 Функция распределения числа очков при бросании кости
Обратите внимание: Хотя случайная величина принимает только дискретные значения ее функция распределения определена для любых х.
Например: F(-1) = 0, F(0) = 0, F(0.999) = 0, F(1.001) = 1/6, F(3.5) = 3/6, F(7) = 1.
Для непрерывных случайных величин вводится понятие плотности распределения р(х), которая есть производная от функци распределения.
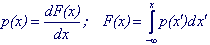 (5.1) (5.1)
Вероятность того, что случайная величина ξ примет значение, лежащее в интервале (а,b) равна разности значений функции распределения на концах интервала
P{ a≤ ξ <b } = F(b) - F(a). (5.2)
Для непрерывных случайных величин
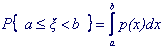 (5.3) (5.3)
Важно помнить, что всегда для дискретных распределений сумма р(хi) по всем возможным значениям хi равна 1;
для непрерывных распределений
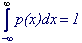 (5.4) (5.4)
|