Web-версия учебного курса "Теория вероятностей"
Раздел 4. Условная вероятность. Независимые события.
Формулы полной вероятности и вероятности гипотез
Если события А и В принадлежат одному полю событий и вероятность В не равна 0, то условной вероятностью А при условии В называется отношение вероятности пересечения А и В к вероятности В.
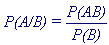 (4.1) (4.1)
Пример 1: Пусть в области, представленной на рисунке 4.1, задана геометрическая вероятность. Событие А - треугольник выше диагонали, событие В - нижняя половина области. Р(А) = 1/2 , Р(В) = 1/2 , Р(АВ) = 1/8 , P(A/B) = 1/4 .
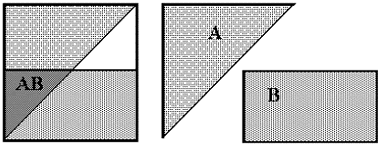
Рисунок 4.1 В квадрате задана геометрическая вероятность
Если P(A/B) = P(A), то события А и В называются независимыми (рисунок 4.2). Для независимых событий из 4.1 следует:
Р(АВ) = Р(А)×Р(В) (4.2)
Это формула "умножения вероятностей", справедливая для независимых событий
Рисунок 4.2 Пример независимых событий A и В
Видно, что АВ составляет такую же долю В, какую А составляет от всего пространства событий.
Формула полной вероятности
Пусть событие А может произойти только совместно с одним из несовместных между собой событий Hi (рисунок ниже), тогда
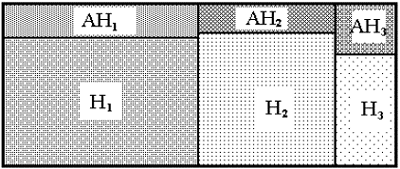
Рисунок 4.3 Вертикальные линии разделяют события H
Р(А) = Р( АН1 ) + Р( АН2 ) + Р( АН3 ) или в общем случае P(A) = Σ P( AHi ) .
Отсюда, используя 4.1, получаем формулу полной вероятности:
 (4.3) (4.3)
Пример 2: Магазин закупает оптом половину всех компьютеров у фирмы LLL, треть - у фирмы МММ и 1/6 - у фирмы NNN. У фирмы LLL 10% компьютеров с браком, у фирмы МММ брак составляет 5%, а у фирмы NNN - 15%. Какова вероятность того, что наудачу выбранный компьютер в этом магазине - бракованный ?
Для решения используем 4.3, положив: Р(Н1) = 1/2, Р(Н2) = 1/3, Р(Н3) = 1/6, Р(А/Н1) = 0.1, Р(А/Н2) = 0.05, Р(А/Н3) = 0.15.
Формула вероятности гипотез
В предыдущем примере можно поставить и другой вопрос. Обнаружен компьютер с браком, какова вероятность, что он получен от фирмы NNN ? Т.е. зная вероятности Р(Нi), которые называются априорные вероятности гипотез Нi, и условные вероятности Р(А/Нi) события А при каждой гипотезе, мы хотим найти апостериорную вероятность какой-либо гипотезы при условии, что событие А произошло: Р(Нi/ А). Формула получается из 4.1, если вместо А подставить туда Нi, а вместо В - А.
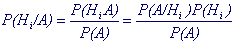 (4.4) (4.4)
Заменив в 4.4 знаменатель формулой полной вероятности 4.3, имеем окончательно:
 (4.5) (4.5)
Пример 3: Студент приходит в медпункт и жалуется на плохое самочувствие, хотя по виду этого не скажешь. У медсестры две гипотезы Н1 - он действительно болен, Н2 - он здоров, но хочет получить справку, например, для продления сессии. По внешнему виду она оценивает априорные вероятности Р(Н1) = 0.3, Р(Н2) = 0.7 и ставит ему градусник. Измеренная температура 37.5 (событие А). Предположим, Р(А/Н1) = 0.9 (не при всякой болезни повышается температура), Р(А/Н2) = 0.05 (у некоторых здоровых людей нормальная температура немного повышена или студент мог незаметно натереть градусник). Теперь апостериорная вероятность того, что студент болен:
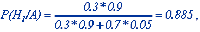
и у медсестры есть все основания направить студента к врачу.
Эксперимент, результат которого существенно изменяет априорные вероятности гипотез, называют информативным. Перед постановкой сложного и (или) дорогостоящего эксперимента всегда имеет смысл оценить его информативность на основе имеющихся данных об априорных и условных вероятностях.
|