Web-версия учебного курса "Теория вероятностей"
Раздел 1. Алгебра событий
Вероятность - свойство случайных событий.
Понятие события - первичное понятие теории - строго не определяется.
Событие - это то, что при определенных условиях может произойти или не произойти. В общем случае событие - это множество элементов. (Иногда - один, иногда - бесконечное множество)
| |
Пример 1 |
Пример 2 |
| Условия : |
бросаем игральную кость |
стрела попала в мишень |
| Событие А : |
выпало четное число очков |
стрела попала в "десятку" |
| Мн-во элементов А : |
2, 4, 6 |
бесконечное множество точек, заполняющих "десятку" |
Событие, которое нельзя разбить на элементы называется элементарным.
В примере 1 - это выпадение определенной грани, скажем - 4.
Событие, которое в данных условиях всегда происходит называется достоверным (U)
В примере 1 - это выпадение любой грани.
Событие, которое в данных условиях никогда не происходит называется невозможным (V)
В примере 1 - это одновременное выпадение двух или более граней при однократном бросании одной кости.
Рассматривая события как множества, можно определить действия над событиями.
a . Объединение событий или сумма событий A U B или А + В - событие,
содержащее все элементы А и В
| | Пример 3 |
|
| Условия : |
бросаем игральную кость |
| Событие А : |
выпало четное число очков |
| Событие B : |
выпало число очков меньше, чем 4 |
 |
| Событие A + B : |
выпало 1, 2, 3, 4 или 6 очков |
| |
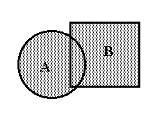
| | Пример 4. См. рисунок 1.1. |
| Событие А : |
круг |
| Событие B : |
квадрат |
| Событие A + B : |
заштриховано |
Рисунок 1.1 |
b . Пересечение событий или произведение событий - A I
B или АВ - событие, содержащее только общие
элементы А и В
| | Пример 5 |
|
| Условия : |
бросаем игральную кость |
| Событие А : |
выпало четное число очков |
 |
| Событие B : |
выпало число очков меньше, чем 4 |
| Событие AB : |
выпало 2 очка |
| |
| |
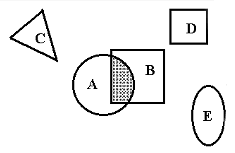
Пример 6. См. рисунок 1.2. |
| Событие А : |
круг |
| Событие B : |
квадрат |
| Событие AB : |
заштриховано |
Рисунок 1.2 |
Если СЕ = V, т.е. пересечение С и Е - пустое множество, события С и Е не имеют общих элементов, то такие события называются несовместными.
На рисунке - несовместные события С, Е, D.
c . Говорят, что событие А влечет за собой событие В (обозачение А c В), если, когда
происходит A, то B обязательно происходит , т.е. все элементы А входят и в В, но В может содержать и элементы,
не входящие в А.
| |
Пример 7 |
Пример 8. См. рисунок 1.2. |
| Условия : |
бросаем игральную кость |
|
| Событие А : |
выпало два очка |
На рисунке 1.2 AB c B |
| Событие B : |
выпало четное число очков |
|
| |
Элементы А входят в В, или A c B |
|
Если А c В и одновременно В c А, т.е. все элементы у А и В - общие, то такие события называются равносильными, или равными.
d . Все элементарные события, в сумме составляющие достоверное образуют пространство элементарных событий. При однократном бросании одной кости пространство элементарных событий содержит 6 элементов, при одновременном бросании двух костей - 36 элементов (всевозможные сочетания числа очков на первой и второй кости), при попадании стрелы в мишень пространство элементарных событий содержит бесконечное множество точек мишени. На рисунках 1 и 2 пространство элементарных событий (достоверное событие) условно обозначено прямоугольником, ограниченным тонкой черной линией и, следовательно содержит все точки этого прямоугольника.
e . Событие, дополняющее данное (А) до достоверного, называется противоположным данному и обозначается чертой сверху (A). Т.е. А + А = U.
f . Все несовместные события, в сумме составляющие достоверное, образуют полную группу событий.
| |
Пример 9 |
| Условия : |
Двое играют шахматную партию. Прошло 2 часа от ее начала. |
| Полная группа событий : |
А - выиграл первый, В - выиграл второй, С - ничья, D - партия еще не закончена. |
Прежде, чем определить вероятность на данном пространстве элементарных событий, строят поле событий. Поле событий - это множество событий, которое включает в качестве элементов :
1 . достоверное событие,
2 . невозможное событие,
3 . все элементарные события данного пространства,
4 . все события, которые на этом пространстве можно построить путем сложения (объединения) событий, путем перемножения (пересечения) событий, а также путем взятия противоположных событий от любого уже построенного.
Таким образом, никакая операция алгебры событий над заданным пространством элементарных событий не порождает события, не принадлежащего полю событий. Поле событий может содержать конечное число элементов (если конечно число элементарных событий) или бесконечное множество событий.
Наиболее строгое и общее определение понятия вероятность дал русский математик А.Н. Колмогоров. Оно гласит :
Каждому событию А из поля событий сопоставляется неотрицательное число Р(А), называемое вероятностью этого события и удовлетворяющее следующим аксиомам:
1. Р(А) ≥ 0 ;
2. Р(U) = 1, U - достоверное событие ;
3. Р(А+В) = Р(А) + Р(В) , если А и В - несовместны.
|
 |
|