Задачи по "Теории вероятностей"

36. В одной из популярных в Америке игр игрок бросает монету с достаточно большого расстояния на поверхность стола, разграфленную на однодюймовые квадраты. Если монета (¾ дюйма в диаметре) попадает полностью внутрь квадрата, то игрок получает награду, в противном случае он теряет свою монету.
    Каковы шансы выиграть при условии, что монета упала на стол?
37. Случайные величины х, у распределены равномерно в интервале 0, 1 и независимы.
    1. Какова вероятность того, что х + у > 0,5 ?
    2. Какова вероятность того, что х - у > 0,5 ?
    3. Построить F(х+у), P(х+у)
    4. Построить F(х-у), P(х-у)
38. Случайная точка А имеет равномерное распределение в квадрате со стороной a (мм).
    Найти вероятность того, что расстояние от А до ближайшей стороны квадрата меньше, чем расстояние от А до ближайшей диагонали квадрата.
39. Плоскость разграфлена параллельными прямыми на расстоянии А друг от друга. На плоскость наугад бросается игла (отрезок) длины l < А.
    Найти вероятность того, что игла пересечет какую-нибудь из прямых.
40. При рентгеновском обследовании вероятность обнаружить заболевание туберкулезом у больного туберкулезом равна P . Вероятность принять здорового человека за больного равна q . Пусть доля больных туберкулезом по отношению ко всему населению равна x.
    Найти условную вероятность того, что человек здоров, если он был признан больным при обследовании.
41. В неполной перетасованной колоде 10 красных карт и 8 черных. Из колоды вынимают карты по одной и выкладывают на стол.
    Найти вероятность р того, что в какой-то момент число вынутых красных карт станет равно числу вынутых черных?
42. А, В и C сходятся для трехсторонней дуэли. известно, что для А вероятность попасть в цель равна 0,3, для C - 0,5, а В стреляет без промаха. Дуэлянты могут стрелять в любого противника по выбору. Первым стреляет А, затем В, дальше C и т.д. в циклическом порядке (раненый выбывает из дуэли), пока лишь один человек не останется невредимым. Какой должна быть стратегия А?
43. Разрыв электрической цепи происходит в том случае, когда выходит из строя хотя бы один из двух последовательно соединенных элементов (x, y) или одновременно оба паралельных сопротивления (P,q).
    Определить вероятность того, что не будет разрыв цепи, если элементы выходят из строя с вероятностями, указанными ниже.
44. В жюри из трех человек два члена независимо друг от друга принимают правильное решение с вероятностью P , а третий для вынесения решения бросает монету (окончательное решение выносится большинством голосов). Жюри из одного человека выносит справедливое решение с вероятностью р.
    Какое из этих жюри выносит справедливое решение с большей вероятностью ?
45. Человек стоит в одном шаге от обрыва и делает шаги к обрыву и от него следующим образом: с вероятностью p к обрыву и с вероятностью (1 - p) = q от него.
    Найти вероятность того, что он когда-нибудь упадет.
46. В первой урне находятся a белыx и b черных шаров, а во второй - n белых и m черныx шаров. Из каждой урны по схеме случайного выбора без возвращения удалили по одному шару, а оставшиеся шары ссыпали в третью урну
    Найти вероятность того, что шар, вынутый из третьей урны, окажется белым.
47. На первом курсе в первой группе 25 студентов, из них 2 стипендиата предприятия; во второй 16 студентов, из них 5 стипендиатов. Наудачу выбран 1 студент.
    Какова вероятность того, что он стипендиат предприятия? Какова вероятность того, что он из 1 группы, если оказалось, что он стипендиат предприятия?
48. В задаче 16 положить, что общее число писем n и конвертов n.
    Каково среднее число писем, попавших к адресатам.
49. Баллон наполнен смесью неона (30%) и гелия (70%). Температура газа 300 К.
    Какова средняя скорость атома в баллоне ? (Газ считать идеальным).
50. Пользуясь определением Мх и Dх, вычислить Мх и Dх
    1. для случайной величины, распределенной равномерно в интерале (а,b)
    2. для случайной величины, распределенной по закону Пуассона с параметром а
    3. для случайных величин, плотность распределения которых представлена на графике
       
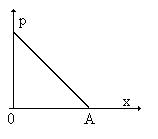
    4. для случайной величины, распределенной по закону Бернулли с параметрами р ,  n
51. Два студента А и В поочередно бросают игральную кость. Выигрывает тот, у которого раньше выпадает пятерка. Начинает А.
    1. найдите закон распределения, математическое ожидание и дисперсию случайной величины, равной числу бросаний кости до окончания игры
    2. найдите вероятность того, что игра закончится при одиннадцатом бросании, если известно, что выиграл студент А
52. При записи программы на неисправном накопителе появляется в среднем 4 ошибки.
    1. какова вероятность безошибочной записи ?
    2. какова вероятность записи с 4 ошибками ?
    4. сколько раз в среднем надо записывать программу, чтобы получить безошибочную запись?
53. Частица движется в разреженном газе, вероятность ее столкновения на пути dl с другой частицей р = Nqdl , где N - концентрация частиц в газе, q - сечение столкновения.
    Найти среднюю длину свободного пробега.
54. Найти вероятность того, что ближайшая частица находится от данной в некоторый момент времени на расстоянии от R до R + dR. Концентрация частиц N.
55. Случайная величина распределена нормально с дисперсией 25 и средним 2.
    Найти вероятность того, что она примет значение в интервале (0,4).
56. Найти вероятность того, что среднее арифметическое 5 независимых случайных величин, каждая из которых распределена нормально с параметрами Мх = 1 , Dх = 4 , лежит в интервале (0.5 ÷ 1.5).
57. Две точки брошены наугад на отрезок 0,L.
    Найти F(r) , P(r) , M(r) , D(r) , где r - расстояние между точками.
58. Построить характеристическую функцию случайной величины, распределенной по закону Пуассона, и показать, что сумма независимых случайных величин, распределенных по закону Пуассона, имеет тоже пуассоновское распределение.
59. Случайная величина х распределена равномерно в интервале (0 ÷ 1).
    Найти вероятность того, что среднее арифметическое 100 значений этой величины лежит в интервале (0,50 ÷ 0,01).
60. В цехе 40 станков. Каждый в среднем дает 1 сбой в час.
    Найти вероятность того, что общее число сбоев за смену не превысит 300. (Сбои считать независимыми).
61. Найти вероятность того, что при 600 бросаниях 2-х костей число выпаданий 12 очков будет не более 17.
62. Для постройки здания нужно забить в землю не менее 300 свай на глубину 5 м. Если свая на меньшей глубине натыкается на камень, ее спиливают и в число несущих свай она не входит. Вероятность "встретить" такой камень в толще земли глубиной dх:  р = N×S×dx, где N - концентрация камней, S - "сечение" камня.
    1. сколько нужно заготовить свай, чтобы с вероятностью 0,95 их хватило на постройку здания, если N = 0,1 м^-3 , S = 2 м² ?
    2. заготовлено 1000 свай. Сколько свай в среднем удается забить при тех же N, S ?
63. Автобусы N 7 и N 6 могут появиться на остановке равновероятно в любой момент от 8.00 до 8.10 независимо друг от друга.
    Каков наиболее вероятный интервал времени между появлением автобусов на остановке?
64. В поселке n жителей. Каждый из них примерно 6 раз в месяц ездит на поезде в город, выбирая дни поездок по случайным мотивам независимо от остальных.
    Какой наименьшей вместимостью должен обладать поезд, чтобы он переполнялся в среднем не чаще одного раза в m дней (поезд ходит раз в сутки, в месяце 30 дней)?
65. Вероятность хотя бы одного попадания в цель при n выстрелах равна P.
    Найти вероятность того, что:
    1. при четырех выстрелах будет три попадания;
    2. ни одного попадания.
    Взять значения P = 0,75 и n = 2.
66. 8 шахматистов участвуют в турнире, среди них двое близнецов. В первом туре все участники разбиваются на пары по жребию.
    Какова вероятность того, что близнецам придется играть друг с другом?
67. Человек получает в день в среднем 6 электронных писем.
    Какова дисперсия числа получаемых писем? Какова вероятность того, что завтра он получит именно n писем?
68. Стеклянная трубка, длиной L cм, запаянная с одного конца, падая, разбивается на 3 части. Считая любые места разлома равновероятными, оцените среднюю длину части с запаянным концом.
69. Стеклянная трубка, длиной L cм, падая, разбивается на 2 части. Считая любые места разлома равновероятными, оцените среднюю длину более короткой части.
70. Из хорошо перетасованной колоды в 52 карты извлекают по одной, возвращают ее и вновь тасуют.
    На каком месте в среднем появится первый туз? Через сколько опытов в среднем туз появится в третий раз?