Фурье-спектрометр - это интерферометр Майкельсона, который освещается исследуемым излучением, одно из зеркал перемещается с постоянной скоростью, а получившаяся на выходе кривая зависимости отсчета фотоприемного устройства от разности хода лучей в плечах интерферометра подвергается Фурье-анализу и тем самым преобразуется в распределение интенсивности по частотам (длинам волн). В некоторых случаях такая сложная методика оказывается более эффективной, чем прямой анализ спектра.
|
|
1. Источник света 2. Фотоприемник 3. Зеркала С.Д.- светоделитель К - компенсатор У - устройство изменения разности хода Л - линзы (не обязательны) |
|
Рис. 3.15. Оптическая схема Фурье-спектрометра |
|
Основное преимущество Фурье-спектрометра перед другими приборами - более полное использование анализируемого излучения. В каждый момент времени фотоприемник воспринимает излучение во всем исследуемом спектральном диапазоне, чем обеспечивается значительно более высокое соотношение сигнал/шум, чем при последовательном сканировании спектра.
Возможность использования интерферометра для измерения спектра основана на однозначной связи спектра и функции временной корреляции оптического сигнала (см. 3-13). Можно также описать действие интерферометра на излучение как на совокупность монохроматических волн.
Оптическая схема Фурье-спектрометра, реализованного на основе двухлучевого интерферометра Майкельсона, приведена на рис. 3.15.
Поток исследуемого излучения делится светоделителем на две волны, которые после прохождения разных оптических путей интерферируют и попадают на фотоприемник.
Результат интерференции для монохроматического излучения есть волна с интенсивностью
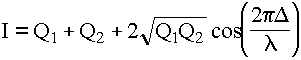 ,
,![]() (3.82)
(3.82)
Q - интенсивность волны в плече интерферометра;
λ - длина волны излучения;
Δ - разность хода лучей.
Предположим, что исходная волна делится на равновеликие части, т.е. Q1 = Q2 = 0.5Q, тогда 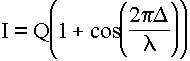 .
.
Если на фотоприемный элемент попадает свет, имеющий спектральное распределение
Q(λ), то отсчет фотоприемника F(Δ) соответствует сумме отсчетов, вызываемых каждой монохроматической составляющей спектра.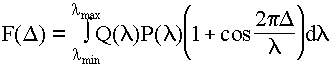 .
.![]() (3.83)
(3.83)
P(λ) - коэффициент пропорциональности между отсчетом и потоком, падающим на приемник, называемый чувствительностью фотоприемника.
Разобьем это выражение на сумму двух интегралов.
Обратим внимание, что второе слагаемое равно первому в случае Δ = 0. Обозначим первое слагаемое
F'(0), а второе - F'(Δ):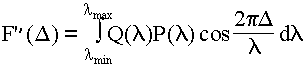
![]() (3.84)
(3.84)
Тогда
F(Δ)=F'(Δ) + F'(0) и F'(Δ) = F(Δ) - 0.5 F(0), т.к. F(0) = 2F'(0).Кривую
F'(Δ) называют интерферограммой.Интерферограмма - это сигнал, регистрируемый в зависимости от изменения оптической разности хода.
Воспользовавшись математическим понятием косинусного преобразования Фурье, видим, что интерферограмма есть косинусный Фурье-образ функции
Q(λ)P(λ) (ограничение пределов интегрирования в конечных величинах в формуле 3.84 возможно, поскольку функция P(λ) отлична от нуля лишь в некотором диапазоне длин волн λmax-λmin).Проведя операцию обратного Фурье-преобразования Ф
-1 интерферограммы и зная кривую чувствительности приемника, можно вычислить спектр:. 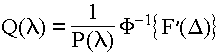 .
.![]() (3.85)
(3.85)
(На самом деле, поскольку мы имеем дело не с полным, а с косинусным Фурье-преобразованием, а они эквивалентны только для симметричных функций, то обратное преобразование восстановит не Q(λ
), a Q(λ) + Q(-λ), но второе слагаемое нас пока не интересует и в дальнейшем для простоты вычислений будем работать не с косинусным, а с экспоненциальным Фурье-преобразованием).Таким образом, процесс получения спектра методом Фурье-спектрометра сводится к следующим этапам:
- измерение
F(Δ) путем регистрации сигнала как функции изменения оптической разности хода;- экспериментальное определение значения
F(0), т.е. регистрация сигнала в точке нулевой разности хода (разность хода в интерферометре будет равна нулю, если оптические длины пути лучей "светоделитель-зеркало" обоих плеч будут равны). Этой точке соответствует абсолютный максимум отсчетов F(Δ);- вычисление обратного преобразования Фурье - выражения
F(Δ) - 0.5 F(0) (выполняется на ЭВМ).В дальнейшем для простоты положим, что Р(λ) = соnst, будем искать только относительное распределение в спектре
J(λ) (так что значение этой константы несущественно), а также для удобства введем новую переменную σ = 1/λ - волновое число.Найдем аппаратную функцию и, следовательно, разрешение Фурье-спектрометра.
Предположим, что прибор освещен монохроматическим светом
J(σ) = δ(σ -σ 0), тогда согласно (3.84):![]()
![]() (3.86)
(3.86)
Здесь Δ
1б Δ2 - пределы, в которых изменялась разность хода в процессе эксперимента. Вне этих пределов отсчеты отсутствуют, т.е. F'(Δ) = 0 вне интервала от Δ1 = -Δmax до Δ2 = Δ max .Обратное преобразование дает:
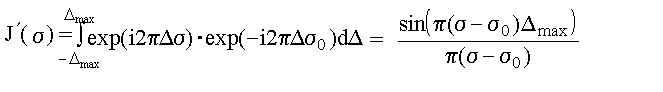
![]() . (3. 87)
. (3. 87)
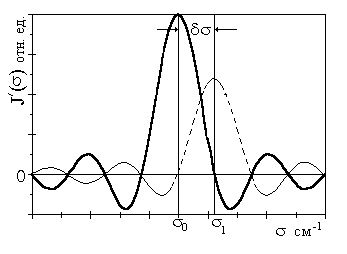
Поскольку это - результат освещения прибора монохроматическим излучением, это и есть аппаратная функция Фурье-спектрометра (рис. 3.16 - сплошная линия). Не следует удивляться, что восстановленный спектр в некоторых местах имеет отрицательные интенсивности. Это не реальные интенсивности, а результат вычислений. За интервал разрешения принимается величина δσ, равная расстоянию от σ
0 до σ1, удовлетворяющая условию δσ = σ0-σ1 = 1/Δ max.|
|
Две спектральные линии считаются разрешенными, если расстояние между ними в шкале волновых чисел не меньше δσ. Разрешаемый интервал длин волн получим, учитывая, что δσ /σ = δλ/λ и то что Δmax = 2L, где L - максимальное перемещение одного из зеркал в процессе эксперимента от положения Δ = 0.
|
|
Рис. 3.16. Аппаратная функция Фурье-спектрометра |
Таким образом, разрешение Фурье-спектрометра зависит от максимальной разности хода в приборе. Теоретически интерферограмма должна быть симметрична относительно точки Δ = 0 (несимметрия говорит о плохой настройке интерферометра), поэтому обычно сканирование начинают незадолго до точки Δ = 0, чтобы только зафиксировать максимум интерферограммы и продолжают до некоторого значения Δ
max. Недостаток аппаратной функции заключается в слишком большой высоте вторичных максимумов, которые могут искажать спектр при наличии в нем линий с разной относительной интенсивностью. Причиной осцилляций служат резкие границы интегрирования в (3.87). Осцилляции можно сгладить, если перед вычислением подынтегральное выражение в (3.87) умножить на некоторую функцию А(Δ), плавно спадающую к границам интегрирования, например, А = 1 - ½2Δ/Δmax½. Эта операция называется аподизацией, она подавляет осцилляции, хотя и ухудшает разрешение.Рабочий диапазон прибора естественно ограничен областью спектральной чувствительности фотоприемника, однако неправильная организация регистрации интерферограммы может его существенно сузить, т.е. будет регистрироваться весь исследуемый спектр, но после Фурье-преобразования возникнет эффект, аналогичный "наложению порядков" или появление "лишних" линий, что не позволит правильно интерпретировать спектр. Понять, чем ограничен рабочий диапазон Фурье-спектрометра, проще всего из такого простого рассуждения.
Если требуется исследовать спектр в диапазоне λ
max-λmin c разрешением δλ (или σmax-σmin с разрешением δσ), надо зарегистрировать не менее М = (λmax-λmin)/δλ отсчетов независимо от способа регистрации. В щелевом приборе это М положений сканирующей системы, последовательно выводящей на выходную щель участки спектра. В Фурье-спектрометре δσ определяется полной длиной интерферограммы, а количество снятых на ней отсчетов, т.е. "шаг" hΔ, т.е. разность хода между точками, в которых снимаются отсчеты, определит полный рабочий диапазон. Математически это следует из того, что к дискретному массиву отсчетов можно применить лишь дискретное Фурье-преобразование, которое восстанавливает периодические функции и, если период окажется меньше спектрального диапазона излучения, попадающего в прибор, тогда и возникает эффект наложения порядков. Строго по выделенному дополнительным фильтром (или чувствительностью приемника, или природой источника) подлежащему исследованию диапазону σmax-σmin интервал между отсчетами на интерферограмме следует определять из условия: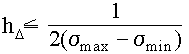 .
. ![]() (3.89)
(3.89)
Требование удвоения периода по сравнению с рабочим диапазоном связано с использованием косинусного преобразования Фурье, которое наряду со спектром J(σ
) восстанавливает спектр J(-σ), который также может создавать нежелательный эффект наложения порядков.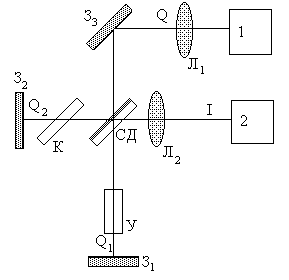
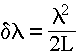 (3.88)
(3.88)