Теорию дифракционной решетки можно найти в учебниках по физической оптике.
|
|
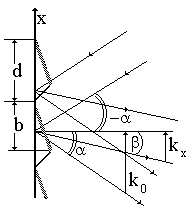
В спектральных приборах используются обычно отражательные и профилированные решетки. Это означает, что отражающие штрихи наклонены под некоторым углом к поверхности решетки (см. рис. 3.9). Смысл такой конструкции прояснится ниже. Вывод аппаратной функции решетки основан на том, что распределение поля по углам (точнее, по проекциям волнового вектора kх) есть Фурье-образ распределения по координате х. Пусть на решетку падает плоская монохроматическая волна под углом α . |
Рис. 3.9. Схема падения и дифракции волны на профилированной решетке |
|
Ось х направим вдоль поверхности решетки перпендикулярно к ее штрихам. Обозначим к
0 х-проекцию волнового вектора волны, зеркально отраженной от поверхности решетки; d - период решетки; b - ширина отражающего штриха; N - полное число штрихов.Наклон штриха ведет к дополнительному набегу фазы волны, пропорциональному расстоянию от х до начала штриха. Обозначим коэффициент пропорциональности q. Тогда поле на решетке (j - номер штриха) :
f(x) = exp(ik0x - iq(x - jd)) при jd ≤ xj ≤ d+b,
f(x) = 0 при jd+b ≤ xj ≤ (j+1)d, ![]() (3.65)
(3.65)
Фурье образ этого поля:
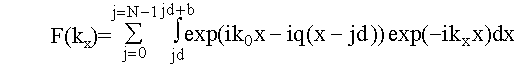 .
. ![]() (3.66)
(3.66)
Выполнив интегрирование и суммирование в (3.66) и вычислив квадрат модуля результата, получим распределение интенсивности по кх в виде двух сомножителей i(kx) = J1*J2, где J1 - результат интерференции волн от N щелей, J
2 - результат дифракции волны на одной щели шириной b.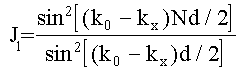 ,
, ![]() (3.67)
(3.67)
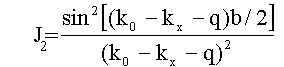 .
. ![]() (3.68)
(3.68)
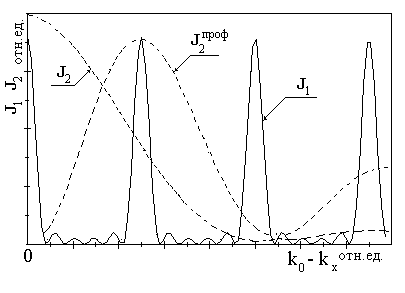
Поскольку kx = (2π/λ) sin β, то i(kx) = J1*J2 дает распределение интенсивности по углам дифракции, что в фокальной плоскости объектива спектрометра превращается в распределение по координатам и поскольку им сопоставлены определенные значения длин волн, то это и есть аппаратная функция прибора с решеткой. Рис. 3.10, 3.11 иллюстрируют эти функции для случаев, когда q = 0 (J2, i - решетка не профилирована, тогда максимальная интенсивность соответствует k0 - kх = 0, т.е. неинформативному нулевому порядку дифракции) и q ≠ 0 (J2проф, iпроф). Профилирование решетки позволяет направить максимум излучения в первый или высшие порядки, где происходит спектральное разложение.
|
|
|
|
Рис. 3.10. Функции J 1, J2 |
Рис. 3.11. Аппаратная функция решетки |
Углы в теории решетки пpинято отсчитывать от нормали к ней, при этом если падающие и дифрагированные лучи лежат по разные стороны от решетки, то им приписываются разные знаки. Условие главных максимумов J
1 (3.67) (k0-kх)d/2 = mπ принимает вид:d (sin α + sin β) = mλ. ![]() (3.69)
(3.69)
Дифференцируя (3.69), легко найти угловую и линейную дисперсию решетки:
dβ/dλ = m/(d cos β), dx/dλ = mF/(d cos β). ![]() (3.70)
(3.70)
Разрешающую способность решетки можно вывести непосредственно из вида аппаратной функции и условия совпадения положений главного максимума порядка m для длины волны λ с ближайшим минимумом для длины волны λ + δλ.
Однако проще воспользоваться общим свойством щелевых приборов (3.62), учтя, что если размер решетки - N
d, то сечение пучка, дифрагированного под углом β, будет D = Ndcos β.Подставив это значение в (3.62), с учетом (3.70) получим:
δλкр = λ/(mN), ![]() (3.71)
(3.71)
Соответственно, предельная разрешающая способность дифракционной решетки
R = λ/δλкр = mN. ![]() (3.72)
(3.72)
При использовании щелей с шириной больше нормальной аппаратная ширина оценивается по общим формулам (3.59), (3.60).
Приборы с решеткой обладают большим разрешением, чем призменные; при незначительной вариации угла β в пределах исследуемого спектра их дисперсия может считаться постоянной, что облегчает градуировку. Существенный недостаток состоит в эффекте наложения порядков: как видно из (3.69), в одном и том же месте оказывается максимум первого порядка для длины волны λ, второго для λ/2, третьего для λ/3 и т.д. Поэтому при исследовании широких спектров, не ограниченных областью спектральной чувствительности фотоприемника, приходится устанавливать перед щелью приборов дополнительные фильтры.
Иногда используют приборы с вогнутой решеткой, штрихи наносятся на сферическую поверхность и такая решетка одновременно выполняет и функции двух объективов прибора [44]. Заметим также, что использование двух объективов в щелевых приборах, вообще говоря, не является принципиальным. Спектр в выходной плоскости можно получить с помощью одного объектива, установленного так, чтобы в выходной плоскости получалось изображение входной щели. Диспергирующий элемент может быть установлен в любом месте между входной и выходной плоскостями, при этом угловая дисперсия определяется этим элементом согласно (3.63), (3.70), а в выражение для линейной дисперсии (3.58) вместо F
2 подставляется расстояние от объектива до выходной плоскости. В промышленных приборах такие схемы не применяются, т.к., как правило, в них сильнее сказываются аберрации и неточности фокусировки.Остановимся теперь на таком "дефекте" щелевых приборов, как "кривизна спектральных линий
".В спектральных приборах с входной прямоугольной щелью на выходе мы не получим идеально прямоугольного изображения, оно получается изогнутым.
В призменных приборах это связано с тем, что для точек, которые лежат на концах щели, расстояние t прохождения света в стекле призмы больше, чем для точек, лежащих на центральном сечении. Согласно формуле (3.58), это приводит к увеличению угловой дисперсии, а т.к. дисперсия стекла растет с уменьшением λ, то концы изображения спектральной линии загибаются в синюю сторону спектра.
Для решетки наблюдается обратный эффект. Волны, исходящие из концов щели, имеют волновой вектор, не лежащий в плоскости, перпендикулярной штрихам решетки (плоскость чертежа 3.9). Проекция волнового вектора на эту плоскость меньше его длины (2π/λ), поэтому эти волны дифрагируют как более длинные и концы изображения спектральной линии загибаются в красную сторону спектра.
В заключение данного раздела следует упомянуть о попытках повысить светосилу щелевых приборов без ухудшения разрешения.
Одним из таких предложений является идея растрового спектрометра
[44, 45].Идеальным был бы прибор с аппаратной функцией в виде δ-функции, т.е. g(x) = δ(x). Поскольку для щелевых приборов с выходной щелью шире ноpмальной аппаратная функция определяется свeрткой пропускания входной и выходной щели, то теоретически, если бы эти пропускания имели вид P(x) = exp(ix2), то свернув эту функцию с такой же, мы бы получили:
![]()
![]() (3.73)
(3.73)
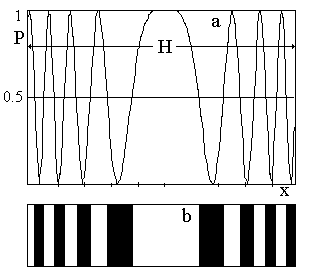
На практике можно реализовать действительную часть функции exp(i
x2), т.е. P(x) = соs(bx2) и свертка приближается к δ-функции тем ближе, чем дальше удастся расширить пределы интегрирования в (3.73).|
Рис. 3.12. а - функция Р(х), b - соответствующий растр на щелях |
Пропускание равно 0 там, где Р(х) ≤ 0.5. Возможны растры и более сложной формы [44, 45], но важно, что светосила такого спектрометра определяется по (3.57), где при определении площади щели ее шириной следует считать половину полной ширины растра Н, а при вычислении аппаратной ширины по (3.62) вместо S подставить ширину самой узкой щели растра (полагаем F1 = F2, растры на входной и выходной щелях одинаковые). |
Еще один вариант попытки увеличить чувствительность установки со щелевым спектрометром к слабым сигналам представляет собой спектрометр с
преобразованием Адамара [45].Входная щель обычная, ширина в зависимости от требуемого разрешения. На выходе получаем спектр, который должен регистрироваться интегрально по всей выходной плоскости, но на него последовательно накладываются различные маски, число которых равно числу подлежащих измерению спектральных интервалов: в каждом j-ом такте работы прибора получаем отсчет системы:
![]() ,
, ![]() (3.74)
(3.74)
где i
i - поток излучения, приходящийся на i-й спектральный интервал, aij - пропускание j-ой маски для i-го спектрального интервала, v - коэффициент пропорциональности между током фотоприемника и падающим на него потоком излучения (предполагается известным).По зарегистрированным F
j и известным аij потоки ii находятся из системы уравнений (3.74). В случае механических масок их элементы аij принимают значения 0 или 1, фотодиодные матрицы в качестве фотоприемника позволяют синтезировать на них матрицы с элементами +1 и -1. В этом случае наилучшими, т.е. обеспечивающими минимальную погрешность при решении (3.74) будут ортогональные маски, построенные как строки матрицы Адамара.Матрица Адамара Н состоит из -1 и +1, все строки и столбцы ее взаимно ортогональны. Принцип построения ее прост: каждая матрица порядка 2n строится из матриц порядка n по правилу (3.75)
 ,
, 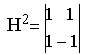 .
. ![]() (3.75)
(3.75)
Описанные "экзотические" щелевые приборы:
растровый и с преобразованием Адамара интересны своей идеей, но не получили широкого распространения, т.к. их основная цель - увеличение светосилы быстрее и естественнее достигается в интерференционных приборах.