3.2.7. Резонансное уширение
Линии, начинающиеся или заканчивающиеся на резонансном уровне, при взаимодействии излучающего атома с атомами того же сорта испытывают уширение, обусловленное резонансной передачей энергии от излучающего к возмущающему атому, что приводит к сокращению времени жизни резонансного уровня и, следовательно, и его уширению.
Рассчитанный в ударном приближении контур φ(ω) имеет дисперсионный вид (3,14) с шириной, которая, вообще говоря, для каждого сорта атомов должна рассчитываться квантовомеханически, но для оценки можно использовать выражение [17]:
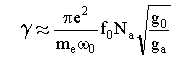 ,
, ![]() (3.30)
(3.30)
где γ - ширина линии в с-1, ω0, f0 - частота и сила осциллятора перехода, связывающего уровни основной (статвес g
0) и резонансный (статвес ga), Na - концентрация атомов того же элемента, что и излучающий, в см-3 (формула в системе CGSE).В статическом приближении, которое справедливо для крыльев линии, где
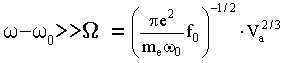 ,
,![]() (3.31)
(3.31)
(Va - средняя относительная скорость атомов), резонансно уширенная линия сохраняет ту же зависимость от
ω-ω0 (3.34), но с несколько большей шириной, чем γ (3.30) [8].3.2.8. Ван-дер-Ваальсовское уширение
Так называют уширение линий посторонними атомами или молекулами или уширение линий в собственном газе для линий, для которых ни верхний, ни нижний уровень не связаны дипольным переходом с основным состоянием. Центр линии, как и для других эффектов давления, описывается в ударном приближении, т.e. линия имеет форму (3.22), где в бинарном приближении
γ = 8.16 C62/5 V3/5 Nаλ2/(2πc), (см) Δ = γ/2.8.![]() (3.32)
(3.32)
Здесь Nа - концентрация возмущающих атомов, V - их средняя относительная скорость, С6 - константа ван-дер-ваальсовского уширения, которая определяет изменение частоты излучения атома Δω при условии, что ближайший "сосед" находится на расстоянии R:
Δω = С6/R6,
С6 = С6i - С6j. ![]() (3.33)
(3.33)
Kонстанта С6k (k = i, j), характеризующая сдвиг k-го уровня под влиянием возмущения, рассчитывается во втором порядке теории возмущений в предположении, что атомы взаимодействуют как два диполя, и может быть представлена в виде
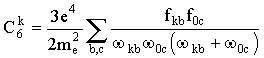 ,
, ![]() (3.34)
(3.34)
где fkb - силы осцилляторов для переходов с одного из уровней данной линии (k) на все другие уровни излучающего атома, f
0c - то же для переходов с основного уровня возмущающего атома на все другие уровни этого атома, ωkb, ω0c - частоты соответствующих переходов.В одноэлектронном приближении
![]()
![]() (3.35)
(3.35)
Формулы даны в системе CGSE, С6 - в см6 c-1, a0 - радиус первой боровской орбиты, n - эффективное главное квантовое числа уровня k, α - поляризуемость возмущающего атома (для некоторых атомов эту величину можно найти в монографии [24] и можно оценить по фомуле α ≈ (4/3) p a0<r2>(Ry/i), где <r2> - средний квадрат радиуса возмущающего атома, р - число эквивалентных электронов в его оболочке, i - потенциал его ионизации, Ry - постоянная Ридберга [7]). Условиe применимости бинарного приближения может быть представлено в виде
![]()
Условиe применимости ударного приближения имеет вид [8]:
ω-ω0 << Ω = V6/5 С6-1/5 ![]() (3.36)
(3.36)
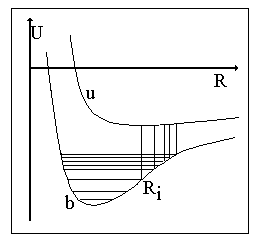
Для расстояний от центра линии, превосходящих Ω, линия имеет "статистическое крыло". Излучение в крыльях может рассматриваться как переходы между термами квазимолекулы, образованной излучающим и возмущающим атомами. Частота перехода при сближении атомов на расстоянии R
![]()
![]() (3.37)
(3.37)
где U
u и Ub - электронные термы квазимолекулы для верхнего (u) и нижнего (b) уровня перехода.Переход к форме контура происходит по формуле, аналогичной (3.27), но с учетом следующих фактов.
При сильном сближении атомов нельзя не учитывать влияния их взаимодействия на взаимное расположение. При выводе формул (3.28), (3.29) положение возмущающей частицы предполагалось равновероятным в любой точке пространства. Однако чтобы подойти очень близко к излучающему атому, ей надо преодолеть его отталкивание (или наоборот, она испытывает притяжение). Поэтому в формуле для φ(ω) появляется "больцмановский фактор". В то же время экспонента не учитывается, т.к. для близких взаимодействий она очень мала, а "сворачивать" ударный и статический контур для одного и того же возмущающего процесса нельзя, т.к. они не являются независимыми. Кроме того, в выражение для φ(ω) включается суммирование по R, т.к. переходы между электронными уровнями молекулы происходят не при любых расстояниях R, а только при отвечающих принципу Франка-Кондона [25] (см. рис 3.1).
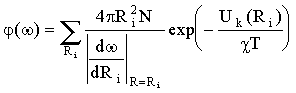 .
.![]() (3.38)
(3.38)
Здесь k = b для контура поглощения и k = u для контура излучения, χ - постоянная Больцмана, Т - температура атомов.
Такое описание предполагает, что потенциальные кривые Uu(R) и Ub(R) или хотя бы одна из них имеют минимум (только в этом случае можно говорить о дискретных "точках Кондона"). При расстояниях, отвечающих минимуму Uu(R) - Ub(R), производная в (3.38) обращается в 0, а φ(ω) - в бесконечность; реально этого не происходит, т.к. состояние с данным R длится конечное время и следует учесть его "размытие".
|
Рис.3.1. Термы квазимолекулы |
Однако на частотах, отвечающих условию dω/dR = 0, на крыле линии возникают локальные максимумы - "сателлиты". Положение сателлитов при определенных предположениях о виде U(R) позволяет оценить параметры потенциала взаимодействия. Hапример, очень часто используется так называемый потенциал Леннарда-Джонса [25], при котором ω-ω0 = С6/R6 - С12/R12. (3.39) Если известна величина С6 (например, из оценок (3.35) или определена экспериментально), то по положению сателлита может быть определена величина С 12: |
С12 = С62 (2Δωs)-1, ![]() (3.40)
(3.40)
где Δωs - расстояние от пика сателлита до центра линии.
Таким образом, если типичные значения С6 - это 10-32 ÷ 10-30 см6 c-1, то С12 имеет порядок 10-71 ÷ 10-77 см12 c-1.
В области частот, лежащей между центром линии и первым сателлитом, потенциал взаимодействия атомов не имеет минимумов и, следовательно, переходы возможны при любых R. Здесь можно учитывать только одно слагаемое в потенциале (3.39), а сумма в (3.38) переходит в интеграл с δ-функцией: δ(R - (Δω/C6)1/6). Оценки показывают, что больцмановским множителем в этом случае также можно пренебречь, т.к.
В этом случае ход контура в статическом крыле имеет вид
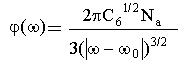 ,
, 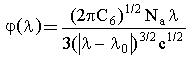 .
. ![]() (3.41)
(3.41)
Общая теория, построенная в [15,16], позволяет описать весь контур, однако уточнения, вносимые описанием промежуточной части контура, несущественно сближают результаты оценок с экспериментом. К сожалению, в эксперименте часто наблюдаются отклонения от предсказанного этой моделью хода крыла даже в области до появления сателлитов.
Так, в работе [27] тщательно измеренный ход крыльев линий Тl 535 нм (переход 7
2S1/2-62P3/2) и 377 нм (переход 72S1/2- 62P3/2), уширенных в атмосфере инертных газов, обнаруживает зависимость вида: φ(ω) ~ (ω-ω0)p, где p принимает значение от 1.3 до 2 в "красном" крыле и от 2 до 3.2 в "синем" для различных уширяющих частиц.Из сказанного можно сделать вывод, что ван-дер-ваальсовское уширение может быть использовано в диагностических целях только в случае, если есть надежные cправочные данные о константах уширения и виде потенциалов взаимодействия. Пока же усилия, в основном, направлены на восстановление вида потенциала по форме контуров [25] и на уточнение теории формирования контура (в частности, путем учета движения возмущающих частиц, перекрытия линий на далеких крыльях и зависимости потенциалов от температуры [13-14]).